Question
Two circles, each of radius 5, have a common tangent at (1, 1) whose equation is $$3x+4y-7=0.$$ Then their centers are :
A.
$$\left( {4,\, - 5} \right),\,\left( { - 2,\,3} \right)$$
B.
$$\left( {4,\, - 3} \right),\,\left( { - 2,\,5} \right)$$
C.
$$\left( {4,\,5} \right),\,\left( { - 2,\, - 3} \right)$$
D.
none of these
Answer :
$$\left( {4,\,5} \right),\,\left( { - 2,\, - 3} \right)$$
Solution :
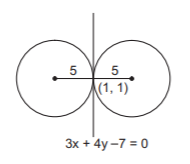
From the figure, the centers are
$$\eqalign{ & \left( {1 \pm 5\cos \,\theta ,\,1 \pm 5\sin \,\theta } \right),{\text{ where}} \cr & \tan \,\theta = - \frac{1}{{ - \frac{3}{4}}} = \frac{4}{3} \cr & {\text{So, }}\cos \,\theta = \frac{3}{5},\,\,\sin \,\theta = \frac{4}{5} \cr} $$

From the figure, the centers are
$$\eqalign{ & \left( {1 \pm 5\cos \,\theta ,\,1 \pm 5\sin \,\theta } \right),{\text{ where}} \cr & \tan \,\theta = - \frac{1}{{ - \frac{3}{4}}} = \frac{4}{3} \cr & {\text{So, }}\cos \,\theta = \frac{3}{5},\,\,\sin \,\theta = \frac{4}{5} \cr} $$