Question
Two blocks of masses $${m_1} = 10\,kg$$ and $${m_2} = 20\,kg$$ are connected by a spring of stiffness $$k = 200\,N/m.$$ The coefficient of friction between the blocks and the fixed horizontal surface is $$\mu = 0.1.$$ Find the minimum constant horizontal force $$F$$ (in newtons) to be applied to $${m_1}$$ in order to slide the mass $${m_2}.$$
A.
$$\mu {m_1}g + \frac{{\mu {m_2}g}}{2}$$
B.
$$\mu {m_1}g + \mu {m_2}g$$
C.
$$\mu {m_1}g - \frac{{\mu {m_2}g}}{2}$$
D.
$$\frac{{\mu {m_1}g + \mu {m_2}g}}{2}$$
Answer :
$$\mu {m_1}g + \frac{{\mu {m_2}g}}{2}$$
Solution :
$${W_F} + {W_{Sp}} + {W_{{\text{fric}}}} = \Delta k$$
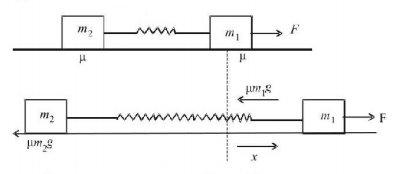
$$\eqalign{ & \Rightarrow F - \frac{1}{2}k{x^2} - \mu {m_1}g\,x = 0\,and\,kx = \mu {m_2}g \cr & \Rightarrow F - \frac{1}{2}\mu {m_2}g - \mu {m_1}g = 0 \Rightarrow F = \mu {m_1}g + \frac{{\mu {m_2}g}}{2} \cr} $$
$${W_F} + {W_{Sp}} + {W_{{\text{fric}}}} = \Delta k$$

$$\eqalign{ & \Rightarrow F - \frac{1}{2}k{x^2} - \mu {m_1}g\,x = 0\,and\,kx = \mu {m_2}g \cr & \Rightarrow F - \frac{1}{2}\mu {m_2}g - \mu {m_1}g = 0 \Rightarrow F = \mu {m_1}g + \frac{{\mu {m_2}g}}{2} \cr} $$