Question
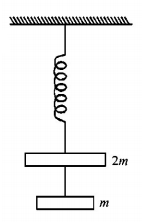
Two blocks $$A$$ and $$B$$ of masses $$3\,m$$ and $$m$$ respectively are connected by a massless and inextensible string. The whole inextensible string. The whole massless spring as shown in figure.
Two blocks $$A$$ and $$B$$ of masses $$3\,m$$ and $$m$$ respectively are connected by a massless and inextensible string. The whole inextensible string. The whole massless spring as shown in figure.
The magnitudes of acceleration of $$A$$ and $$B$$ immediately after the string is cut, are respectively :

A.
$$\frac{g}{3},g$$
B.
$$g,g$$
C.
$$\frac{g}{3},\frac{g}{3}$$
D.
$$g,\frac{g}{3}$$
Answer :
$$\frac{g}{3},g$$
Solution :

Before cutting the string
$$\eqalign{ & kx = T + 3mg\,......\left( {\text{i}} \right) \cr & T = mg\,......\left( {{\text{ii}}} \right) \cr & \Rightarrow kx = 4mg \cr} $$

After cutting the string
$$\eqalign{ & T = 0 \cr & {a_A} = \frac{{4mg - 3mg}}{{3m}} \cr & {a_A} = \frac{g}{3} \uparrow \,\,{\text{and}}\,\,{a_B} = \frac{{mg}}{m} = g \downarrow \cr} $$

Before cutting the string
$$\eqalign{ & kx = T + 3mg\,......\left( {\text{i}} \right) \cr & T = mg\,......\left( {{\text{ii}}} \right) \cr & \Rightarrow kx = 4mg \cr} $$

After cutting the string
$$\eqalign{ & T = 0 \cr & {a_A} = \frac{{4mg - 3mg}}{{3m}} \cr & {a_A} = \frac{g}{3} \uparrow \,\,{\text{and}}\,\,{a_B} = \frac{{mg}}{m} = g \downarrow \cr} $$