Question
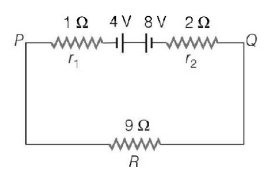
Two batteries of emf $$4\,V$$ and $$8\,V$$ with internal resistance $$1\,\Omega $$ and $$2\,\Omega $$ are connected in a circuit with a resistance of $$9\,\Omega $$ as shown in figure. The current and potential difference between the points $$P$$ and $$Q$$ are
Two batteries of emf $$4\,V$$ and $$8\,V$$ with internal resistance $$1\,\Omega $$ and $$2\,\Omega $$ are connected in a circuit with a resistance of $$9\,\Omega $$ as shown in figure. The current and potential difference between the points $$P$$ and $$Q$$ are
A.
$$\frac{1}{3}A\,{\text{and}}\,3\,V$$
B.
$$\frac{1}{6}A\,{\text{and}}\,4\,V$$
C.
$$\frac{1}{9}A\,{\text{and}}\,9\,V$$
D.
$$\frac{1}{{12}}A\,{\text{and}}\,12\,V$$
Answer :
$$\frac{1}{3}A\,{\text{and}}\,3\,V$$
Solution :
Applying Kirchhoff's voltage law in the given loop and going in direction of current $$PSTQ$$ total voltage is equal to zero
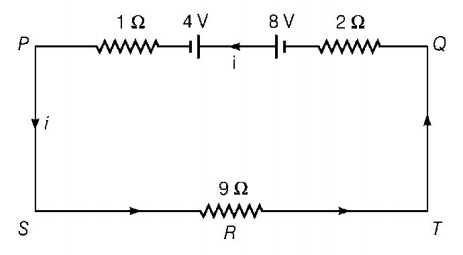
So, $$ - 2i + 8 - 4 - 1 \times i - 9i = 0$$
$$\therefore i = \frac{1}{3}A$$
Potential difference across $$PQ = \frac{1}{3} \times 9$$
$$ = 3\,V$$
Applying Kirchhoff's voltage law in the given loop and going in direction of current $$PSTQ$$ total voltage is equal to zero

So, $$ - 2i + 8 - 4 - 1 \times i - 9i = 0$$
$$\therefore i = \frac{1}{3}A$$
Potential difference across $$PQ = \frac{1}{3} \times 9$$
$$ = 3\,V$$
