Question
Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in $$sq. m$$ ) of the flower-bed, is:
A.
30
B.
12.5
C.
10
D.
25
Answer :
25
Solution :
$$\eqalign{ & {\text{We have}} \cr & {\text{Total length}} = r + r + r\theta = 20 \cr & \Rightarrow 2r + r\theta = 20 \cr & \Rightarrow \theta = \frac{{20 - 2r}}{r}\,......\left( 1 \right) \cr & A = {\text{Area}} = \frac{\theta }{{2\pi }} \times \pi {r^2} = \frac{1}{2}{r^2}\theta = \frac{1}{2}{r^2}\left( {\frac{{20 - 2r}}{r}} \right) \cr & A = 10r - {r^2} \cr & {\text{For}}\,A\,{\text{to}}\,{\text{be}}\,{\text{maximum}}\,\frac{{dA}}{{dr}} = 0 \Rightarrow 10 - 2r = 0 \Rightarrow r = 5 \cr & \frac{{{d^2}A}}{{d{r^2}}} = - 2 < 0 \cr} $$
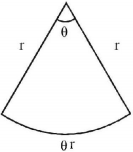
$$\eqalign{ & \therefore \,\,{\text{For}}\,r = 5\,A\,{\text{is}}\,{\text{maximum}} \cr & {\text{From}}\,\left( 1 \right) \cr & \theta = \frac{{20 - 2\left( 5 \right)}}{5} = \frac{{10}}{5} = 2 \cr & A = \frac{2}{{2\pi }} \times \pi {\left( 5 \right)^2} = 25\,sq.m. \cr} $$
$$\eqalign{ & {\text{We have}} \cr & {\text{Total length}} = r + r + r\theta = 20 \cr & \Rightarrow 2r + r\theta = 20 \cr & \Rightarrow \theta = \frac{{20 - 2r}}{r}\,......\left( 1 \right) \cr & A = {\text{Area}} = \frac{\theta }{{2\pi }} \times \pi {r^2} = \frac{1}{2}{r^2}\theta = \frac{1}{2}{r^2}\left( {\frac{{20 - 2r}}{r}} \right) \cr & A = 10r - {r^2} \cr & {\text{For}}\,A\,{\text{to}}\,{\text{be}}\,{\text{maximum}}\,\frac{{dA}}{{dr}} = 0 \Rightarrow 10 - 2r = 0 \Rightarrow r = 5 \cr & \frac{{{d^2}A}}{{d{r^2}}} = - 2 < 0 \cr} $$

$$\eqalign{ & \therefore \,\,{\text{For}}\,r = 5\,A\,{\text{is}}\,{\text{maximum}} \cr & {\text{From}}\,\left( 1 \right) \cr & \theta = \frac{{20 - 2\left( 5 \right)}}{5} = \frac{{10}}{5} = 2 \cr & A = \frac{2}{{2\pi }} \times \pi {\left( 5 \right)^2} = 25\,sq.m. \cr} $$