Question
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$ and $${90^ \circ }C$$ respectively. The temperature of the junction of the three rods will be
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$ and $${90^ \circ }C$$ respectively. The temperature of the junction of the three rods will be

A.
$${45^ \circ }C$$
B.
$${60^ \circ }C$$
C.
$${30^ \circ }C$$
D.
$${20^ \circ }C$$
Answer :
$${60^ \circ }C$$
Solution :
Let $${\theta ^ \circ }C$$ be the temperature at $$B.$$ Let $$Q$$ is the heat flowing per second from $$A$$ to $$B$$ on account of temperature difference.
$$\therefore \,\,Q = \frac{{KA\left( {90 - \theta } \right)}}{\ell }\,\,\,.....\left( {\text{i}} \right)$$
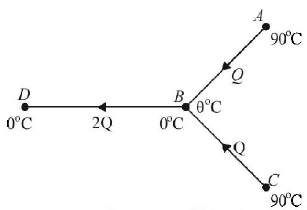
By symmetry, the same will be the case for heat flow from $$C$$ to $$B.$$
∴ The heat flowing per second from $$B$$ to $$D$$ will be
$$2\,Q = \frac{{KA\left( {\theta - 0} \right)}}{\ell }\,\,\,\,.....\left( {{\text{ii}}} \right)$$
Dividing eq. (ii) by eq. (i)
$$\eqalign{ & 2 = \frac{\theta }{{90 - \theta }} \cr & \Rightarrow \,\,\theta = {60^ \circ } \cr} $$
Let $${\theta ^ \circ }C$$ be the temperature at $$B.$$ Let $$Q$$ is the heat flowing per second from $$A$$ to $$B$$ on account of temperature difference.
$$\therefore \,\,Q = \frac{{KA\left( {90 - \theta } \right)}}{\ell }\,\,\,.....\left( {\text{i}} \right)$$

By symmetry, the same will be the case for heat flow from $$C$$ to $$B.$$
∴ The heat flowing per second from $$B$$ to $$D$$ will be
$$2\,Q = \frac{{KA\left( {\theta - 0} \right)}}{\ell }\,\,\,\,.....\left( {{\text{ii}}} \right)$$
Dividing eq. (ii) by eq. (i)
$$\eqalign{ & 2 = \frac{\theta }{{90 - \theta }} \cr & \Rightarrow \,\,\theta = {60^ \circ } \cr} $$