Question
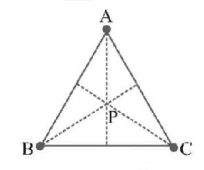
Three equal masses (each $$m$$) are placed at the comers of an equilateral triangle of side $$'a'.$$ Then the escape velocity of an object from the circumcentre $$P$$ of triangle is :
Three equal masses (each $$m$$) are placed at the comers of an equilateral triangle of side $$'a'.$$ Then the escape velocity of an object from the circumcentre $$P$$ of triangle is :
A.
$$\sqrt {\frac{{2\sqrt 3 Gm}}{a}} $$
B.
$$\sqrt {\frac{{\sqrt 3 Gm}}{a}} $$
C.
$$\sqrt {\frac{{6\sqrt 3 Gm}}{a}} $$
D.
$$\sqrt {\frac{{3\sqrt 3 Gm}}{a}} $$
Answer :
$$\sqrt {\frac{{6\sqrt 3 Gm}}{a}} $$
Solution :
$$\eqalign{ & \frac{{ - Gmm'}}{r} \times 3 + \frac{1}{2}m'v_e^2 = 0 \cr & {\text{or}}\,\,\frac{{ - 3Gm}}{{\left( {\frac{{\frac{a}{2}}}{{\cos {{30}^ \circ }}}} \right)}} + \frac{1}{2}v_e^2 = 0 \cr & {v_e} = \sqrt {\frac{{6\sqrt 3 Gm}}{a}} . \cr} $$
$$\eqalign{ & \frac{{ - Gmm'}}{r} \times 3 + \frac{1}{2}m'v_e^2 = 0 \cr & {\text{or}}\,\,\frac{{ - 3Gm}}{{\left( {\frac{{\frac{a}{2}}}{{\cos {{30}^ \circ }}}} \right)}} + \frac{1}{2}v_e^2 = 0 \cr & {v_e} = \sqrt {\frac{{6\sqrt 3 Gm}}{a}} . \cr} $$