Question
Three circles of radii $$a, b, c (a < b < c)$$ touch each other externally. If they have $$x$$ - axis as a common tangent, then:
A.
$$\frac{1}{{\sqrt a }} = \frac{1}{{\sqrt b }} + \frac{1}{{\sqrt c }}$$
B.
$$\frac{1}{{\sqrt b }} = \frac{1}{{\sqrt a }} + \frac{1}{{\sqrt c }}$$
C.
$$a, b, c$$ are in A.P.
D.
$$\sqrt a ,\sqrt b ,\sqrt c {\text{ are in A}}{\text{.P}}{\text{.}}$$
Answer :
$$\frac{1}{{\sqrt a }} = \frac{1}{{\sqrt b }} + \frac{1}{{\sqrt c }}$$
Solution :
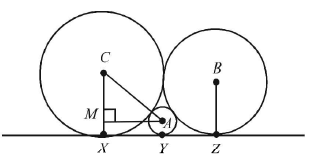
$$\eqalign{ & A{M^2} = A{C^2} - M{C^2} \cr & = {\left( {a + c} \right)^2} - {\left( {a - c} \right)^2} = 4ac \cr & \Rightarrow \,\,A{M^2} = X{Y^2} = 4ac \cr & \Rightarrow \,\,XY = 2\sqrt {ac} \cr & {\text{Similarly,}}\,\,YZ = 2\sqrt {ba} \,\,{\text{and}}\,XZ = 2\sqrt {bc} \cr & {\text{Then,}}\,\,\,\,\,\,\,\,\,\,\,XZ = XY + YZ \cr & \Rightarrow \,\,2\sqrt {bc} = 2\sqrt {ac} + 2\sqrt {ba} \cr & \Rightarrow \,\,\frac{1}{{\sqrt a }} = \frac{1}{{\sqrt b }} + \frac{1}{{\sqrt c }} \cr} $$

$$\eqalign{ & A{M^2} = A{C^2} - M{C^2} \cr & = {\left( {a + c} \right)^2} - {\left( {a - c} \right)^2} = 4ac \cr & \Rightarrow \,\,A{M^2} = X{Y^2} = 4ac \cr & \Rightarrow \,\,XY = 2\sqrt {ac} \cr & {\text{Similarly,}}\,\,YZ = 2\sqrt {ba} \,\,{\text{and}}\,XZ = 2\sqrt {bc} \cr & {\text{Then,}}\,\,\,\,\,\,\,\,\,\,\,XZ = XY + YZ \cr & \Rightarrow \,\,2\sqrt {bc} = 2\sqrt {ac} + 2\sqrt {ba} \cr & \Rightarrow \,\,\frac{1}{{\sqrt a }} = \frac{1}{{\sqrt b }} + \frac{1}{{\sqrt c }} \cr} $$