Question
Three boys and three girls are to be seated around a table, in a circle. Among them, the boy $$X$$ does not want any girl neighbour and the girls $$Y$$ does not want any boy neighbour. The number of such arrangements possible is
A.
4
B.
6
C.
8
D.
None of these
Answer :
4
Solution :
As shown in figure 1, 2 and $$X$$ are the three boys and 3, 4 and $$Y$$ are three girls, Boy $$X$$ will have neighbours as boys 1 and 2 and the girl $$Y$$ will have neighbours as girls 3 and 4.
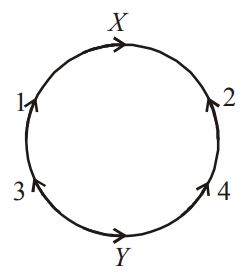
1 and 2 can be arranged in $$P\left( {2,2} \right)$$ ways
$$ = 2! = 2 \times 1 = 2{\text{ ways}}$$
Also, 3 and 4 can be arranged in $$P\left( {2,2} \right)$$ ways
$$ = 2! = 2 \times 1 = 2{\text{ ways}}$$
Hence, required no. of permutations $$= 2 \times 2 = 4$$
As shown in figure 1, 2 and $$X$$ are the three boys and 3, 4 and $$Y$$ are three girls, Boy $$X$$ will have neighbours as boys 1 and 2 and the girl $$Y$$ will have neighbours as girls 3 and 4.

1 and 2 can be arranged in $$P\left( {2,2} \right)$$ ways
$$ = 2! = 2 \times 1 = 2{\text{ ways}}$$
Also, 3 and 4 can be arranged in $$P\left( {2,2} \right)$$ ways
$$ = 2! = 2 \times 1 = 2{\text{ ways}}$$
Hence, required no. of permutations $$= 2 \times 2 = 4$$