The vector $$\overrightarrow c $$ directed along the bisectors of the angle between the vectors $$\overrightarrow a = 7\hat i - 4\hat j - 4\hat k,\,\overrightarrow b = - 2\hat i - \hat j + 2\hat k$$        and $$\left| {\overrightarrow c } \right| = 3\sqrt 6 $$   is given by :

Solution :

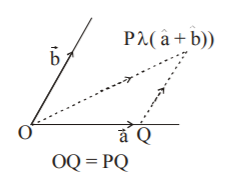
$$\eqalign{ & OQ = PQ = \lambda \,\,\,\left( {{\text{say}}} \right)\,; \cr & \overrightarrow {OP} = \overrightarrow {OQ} + \overrightarrow {QP} \,;\,\overrightarrow c = \lambda \hat a + \lambda \hat b \cr} $$
Let $${\hat a}$$ and $${\hat b}$$ be unit vectors along $$\overrightarrow a $$ and $$\overrightarrow b $$ respectively,
then, $$\hat a = \frac{1}{9}\left( {7\hat i - 4\hat j - 4\hat k} \right)$$     and $$\hat b = \frac{1}{3}\left( { - 2\hat i - \hat j + 2\hat k} \right)$$
The required vector
$$\overrightarrow c = \lambda \left( {\hat a + \hat b} \right),$$    where $$\lambda $$ is a scalar
$$\eqalign{ & \Rightarrow \overrightarrow c = \lambda \left( {\frac{1}{9}\hat i - \frac{7}{9}\hat j + \frac{2}{9}\hat k} \right) \cr & \Rightarrow {\left| {\overrightarrow c } \right|^2} = {\lambda ^2}\left( {\frac{1}{{81}} + \frac{{49}}{{81}} + \frac{4}{{81}}} \right) \cr & \Rightarrow {\left| {\overrightarrow c } \right|^2} = \frac{{54}}{{81}}{\lambda ^2} \cr & \Rightarrow {\left( {3\sqrt 6 } \right)^2} = \frac{{54}}{{81}}{\lambda ^2} \cr & \Rightarrow {\lambda ^2} = 81 \cr & \Rightarrow \lambda = \pm 9 \cr} $$
Hence, $$\overrightarrow c = \left( {\hat i - 7\hat j + 2\hat k} \right)$$