Question
The values of $$\theta \in \left( {0,2\pi } \right)$$ for which $$2{\sin ^2}\theta - 5\sin \theta + 2 > 0,$$ are
A.
$$\left( {0,\frac{\pi }{6}} \right) \cup \left( {\frac{{5\pi }}{6},2\pi } \right)$$
B.
$$\left( {\frac{\pi }{8},\frac{{5\pi }}{6}} \right)$$
C.
$$\left( {0,\frac{\pi }{8}} \right) \cup \left( {\frac{\pi }{6},\frac{{5\pi }}{6}} \right)$$
D.
$$\left( {\frac{{41\pi }}{48},\pi } \right)$$
Answer :
$$\left( {0,\frac{\pi }{6}} \right) \cup \left( {\frac{{5\pi }}{6},2\pi } \right)$$
Solution :
$$\eqalign{ & 2{\sin ^2}\theta - 5\sin \theta + 2 > 0 \cr & \Rightarrow \,\,\left( {\sin \theta - 2} \right)\left( {2\sin \theta - 1} \right) > 0 \cr & \Rightarrow \,\,\sin \theta < \frac{1}{2}\,\,\,\,\,\,\left[ {\because \,\, - 1 \leqslant \sin \theta \leqslant 1} \right] \cr} $$
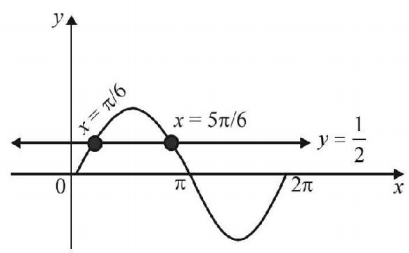
From graph, we get $$x \in \left( {0,\frac{\pi }{6}} \right) \cup \left( {\frac{{5\pi }}{6},2\pi } \right)$$
$$\eqalign{ & 2{\sin ^2}\theta - 5\sin \theta + 2 > 0 \cr & \Rightarrow \,\,\left( {\sin \theta - 2} \right)\left( {2\sin \theta - 1} \right) > 0 \cr & \Rightarrow \,\,\sin \theta < \frac{1}{2}\,\,\,\,\,\,\left[ {\because \,\, - 1 \leqslant \sin \theta \leqslant 1} \right] \cr} $$

From graph, we get $$x \in \left( {0,\frac{\pi }{6}} \right) \cup \left( {\frac{{5\pi }}{6},2\pi } \right)$$