Question
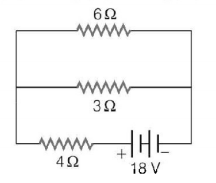
The total power dissipated in watts in the circuit shown here is
The total power dissipated in watts in the circuit shown here is
A.
16
B.
40
C.
54
D.
4
Answer :
54
Solution :
The resistance of $$6\,\Omega $$ and $$3\,\Omega $$ are in parallel in the given circuit, their equivalent resistance is
$$\eqalign{ & \frac{1}{{{R_1}}} = \frac{1}{6} + \frac{1}{3} = \frac{{1 + 2}}{6} = \frac{1}{2} \cr & {\text{or}}\,\,{R_1} = 2\,\Omega \cr} $$
Again, $${R_1}$$ is in series with $$4\,\Omega $$ resistance, hence
$$R = {R_1} + 4 = 2 + 4 = 6\,\Omega $$
Thus, the total power dissipated in the circuit
$$P = \frac{{{V^2}}}{R}$$
Here, $$V = 18\,V,R = 6\,\Omega $$
Thus, $$P = \frac{{{{\left( {18} \right)}^2}}}{6} = 54\,W$$
The resistance of $$6\,\Omega $$ and $$3\,\Omega $$ are in parallel in the given circuit, their equivalent resistance is
$$\eqalign{ & \frac{1}{{{R_1}}} = \frac{1}{6} + \frac{1}{3} = \frac{{1 + 2}}{6} = \frac{1}{2} \cr & {\text{or}}\,\,{R_1} = 2\,\Omega \cr} $$
Again, $${R_1}$$ is in series with $$4\,\Omega $$ resistance, hence
$$R = {R_1} + 4 = 2 + 4 = 6\,\Omega $$
Thus, the total power dissipated in the circuit
$$P = \frac{{{V^2}}}{R}$$
Here, $$V = 18\,V,R = 6\,\Omega $$
Thus, $$P = \frac{{{{\left( {18} \right)}^2}}}{6} = 54\,W$$
