The total number of local maxima and local minima of the function $$f(x) = \left\{ {_{{x^{\frac{2}{3}}},}^{{{(2 + x)}^3},}\,_{ - 1 < x < 2}^{ - 3 < x \leqslant - 1}} \right.\,{\text{is}}$$

Solution :

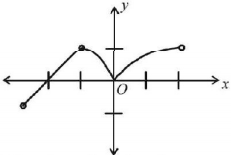
The given function is $$f(x) = \left\{ {_{{x^{\frac{2}{3}}},}^{{{(2 + x)}^3},}\,_{ - 1 < x < 2}^{ - 3 < x \leqslant - 1}} \right.$$
The graph of $$y = f\left( x \right)$$   is as shown in the figure. From graph, clearly, there is one local maximum $$\left( {{\text{at}}\,x = - 1} \right)$$   and one local minima $$\left( {{\text{at}}\,x = 0} \right)$$
∴ total number of local maxima or minima = 2.