Question
The speed of a boat is $$5\,km/h$$ in still water. It crosses a river of width $$1.0\,km$$ along the shortest possible path in $$15\,min.$$ The velocity of the river water is (in $$km/h$$ )
A.
5
B.
1
C.
3
D.
4
Answer :
3
Solution :
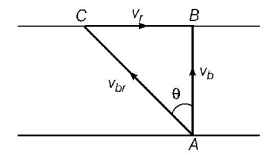
Let $${v_r} =$$ velocity of river
$${v_{br}} =$$ velocity of boat in still water and
$$w =$$ width of river
Time taken to cross the river = $$15\,\min$$
$$ = \frac{{15}}{{60}}h = \frac{1}{4}h$$
Shortest path is taken when $${v_b}$$ is along $$AB.$$ In this case,
$$\eqalign{ & v_{br}^2 = v_r^2 + v_b^2 \cr & {\text{Now,}}\,t = \frac{w}{{{v_b}}} = \frac{w}{{\sqrt {v_{br}^2 - v_r^2} }} \cr & \therefore \frac{1}{4} = \frac{1}{{\sqrt {{5^2} - v_r^2} }} \cr & \Rightarrow {5^2} - v_r^2 = 16 \cr & \Rightarrow v_r^2 = 25 - 16 = 9 \cr & \therefore {v_r} = \sqrt 9 = 3\,km/h \cr} $$
Alternative
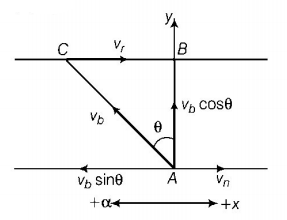
$$\eqalign{ & t = \frac{{15}}{{60}} = \frac{1}{4}\lambda s \cr & \Rightarrow {\text{Motion along the }}Y{\text{ - axis}}\,t = \frac{y}{{{v_b}\cos \theta }} \cr & \Rightarrow \frac{1}{4} = \frac{1}{{5\cos \theta }} \Rightarrow \cos \theta = \frac{4}{5} \cr & {\text{so,}}\,\,\sin \theta = \frac{3}{5} \cr} $$
$$ \Rightarrow $$ Motion is along the $$x$$-axis. For the boat to reach at $$B$$
$$\eqalign{ & {v_b}\sin \theta = {v_r} \cr & \Rightarrow 5 \times \frac{3}{5} = {v_r} \cr & \Rightarrow {v_r} = 3\,km/h \cr} $$
NOTE
If $${v_r} \geqslant {v_{br}},$$ the boatman can never reach at point $$B.$$

Let $${v_r} =$$ velocity of river
$${v_{br}} =$$ velocity of boat in still water and
$$w =$$ width of river
Time taken to cross the river = $$15\,\min$$
$$ = \frac{{15}}{{60}}h = \frac{1}{4}h$$
Shortest path is taken when $${v_b}$$ is along $$AB.$$ In this case,
$$\eqalign{ & v_{br}^2 = v_r^2 + v_b^2 \cr & {\text{Now,}}\,t = \frac{w}{{{v_b}}} = \frac{w}{{\sqrt {v_{br}^2 - v_r^2} }} \cr & \therefore \frac{1}{4} = \frac{1}{{\sqrt {{5^2} - v_r^2} }} \cr & \Rightarrow {5^2} - v_r^2 = 16 \cr & \Rightarrow v_r^2 = 25 - 16 = 9 \cr & \therefore {v_r} = \sqrt 9 = 3\,km/h \cr} $$
Alternative

$$\eqalign{ & t = \frac{{15}}{{60}} = \frac{1}{4}\lambda s \cr & \Rightarrow {\text{Motion along the }}Y{\text{ - axis}}\,t = \frac{y}{{{v_b}\cos \theta }} \cr & \Rightarrow \frac{1}{4} = \frac{1}{{5\cos \theta }} \Rightarrow \cos \theta = \frac{4}{5} \cr & {\text{so,}}\,\,\sin \theta = \frac{3}{5} \cr} $$
$$ \Rightarrow $$ Motion is along the $$x$$-axis. For the boat to reach at $$B$$
$$\eqalign{ & {v_b}\sin \theta = {v_r} \cr & \Rightarrow 5 \times \frac{3}{5} = {v_r} \cr & \Rightarrow {v_r} = 3\,km/h \cr} $$
NOTE
If $${v_r} \geqslant {v_{br}},$$ the boatman can never reach at point $$B.$$




