Question
The solution set of $$\frac{{{x^2} - 3x + 4}}{{x + 1}} > 1,x \in R,$$ is
A.
$$\left( {3, + \infty } \right)$$
B.
$$\left( { - 1,1} \right) \cup \left( {3, + \infty } \right)$$
C.
$$\left[ { - 1,1} \right] \cup \left[ {3, + \infty } \right)$$
D.
None of these
Answer :
$$\left( { - 1,1} \right) \cup \left( {3, + \infty } \right)$$
Solution :
$$\eqalign{ & \frac{{{x^2} - 3x + 4}}{{x + 1}} > 1 \cr & \Rightarrow \,\,\frac{{{x^2} - 4x + 3}}{{x + 1}} > 0 \cr & \Rightarrow \,\,\left( {x - 1} \right)\left( {x - 3} \right)\left( {x + 1} \right) > 0,x \ne - 1\left\{ {{\text{multiplying by }}{{\left( {x + 1} \right)}^2}} \right\} \cr} $$
∴ from general sign scheme:
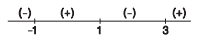
$$\left\{ {\because \,\,{\text{for }}x = 0,\,{\text{expression}} > 0} \right\}.$$
$$\eqalign{ & \frac{{{x^2} - 3x + 4}}{{x + 1}} > 1 \cr & \Rightarrow \,\,\frac{{{x^2} - 4x + 3}}{{x + 1}} > 0 \cr & \Rightarrow \,\,\left( {x - 1} \right)\left( {x - 3} \right)\left( {x + 1} \right) > 0,x \ne - 1\left\{ {{\text{multiplying by }}{{\left( {x + 1} \right)}^2}} \right\} \cr} $$
∴ from general sign scheme:

$$\left\{ {\because \,\,{\text{for }}x = 0,\,{\text{expression}} > 0} \right\}.$$