Question
The slopes of isothermal and adiabatic curves are related as
A.
isothermal curve slope $$=$$ adiabatic curve slope
B.
isothermal curve slope $$ = \gamma \times $$ adiabatic curve slope
C.
adiabatic curve slope $$ = \gamma \times $$ isothermal curve slope
D.
adiabatic curve slope $$ = \frac{1}{2} \times $$ isothermal curve slope
Answer :
adiabatic curve slope $$ = \gamma \times $$ isothermal curve slope
Solution :
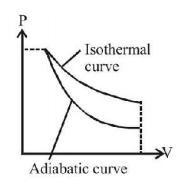
$$\frac{{{\text{Slope}}\,{\text{of}}\,{\text{adiabatic}}\,{\text{curve}}}}{{{\text{Slope}}\,{\text{of}}\,{\text{isothermal}}\,{\text{curve}}}} = \frac{{{{\left( {\frac{{dP}}{{dV}}} \right)}_{{\text{adi}}}}}}{{{{\left( {\frac{{dP}}{{dV}}} \right)}_{{\text{iso}}}}}} = + \gamma $$
So slope to adiabatic curve is $$\gamma \left( { = \frac{{{C_p}}}{{{C_v}}}} \right)$$ times of isothermal curve, as clear also from figure.

$$\frac{{{\text{Slope}}\,{\text{of}}\,{\text{adiabatic}}\,{\text{curve}}}}{{{\text{Slope}}\,{\text{of}}\,{\text{isothermal}}\,{\text{curve}}}} = \frac{{{{\left( {\frac{{dP}}{{dV}}} \right)}_{{\text{adi}}}}}}{{{{\left( {\frac{{dP}}{{dV}}} \right)}_{{\text{iso}}}}}} = + \gamma $$
So slope to adiabatic curve is $$\gamma \left( { = \frac{{{C_p}}}{{{C_v}}}} \right)$$ times of isothermal curve, as clear also from figure.
