Question
The slope of the tangent to a curve $$y = f\left( x \right)$$ at $$\left( {x,\,f\left( x \right)} \right)$$ is $$2x + 1.$$ If the curve passes through the point $$\left( {1,\,2} \right),$$ then the area of the region bounded by the curve, the $$x$$-axis and the line $$x = 1$$ is :
A.
$$\frac{5}{6}{\text{ sq}}{\text{. unit}}$$
B.
$$\frac{6}{5}{\text{ sq}}{\text{. unit}}$$
C.
$$\frac{1}{6}{\text{ sq}}{\text{. unit}}$$
D.
$$6{\text{ sq}}{\text{. unit}}$$
Answer :
$$\frac{5}{6}{\text{ sq}}{\text{. unit}}$$
Solution :
We, given $$\frac{{dy}}{{dx}} = 2x + 1 \Rightarrow y = {x^2} + x + k$$
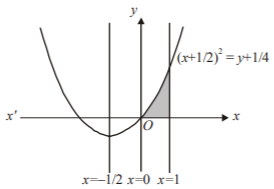
Since, the curve passes through the point $$\left( {1,\,2} \right)$$
$$\eqalign{ & \therefore \,2 = 1 + 1 + k \Rightarrow k = 0 \cr & \therefore \,{\text{The curve is }}y = {x^2} + x \cr} $$
So, the required area
$$\eqalign{ & = \int_0^1 {\left( {{x^2} + x} \right)dx} \cr & = \left[ {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right]_0^1 \cr & = \frac{1}{3} + \frac{1}{2} \cr & = \frac{5}{6}{\text{ sq}}{\text{. unit}} \cr} $$
We, given $$\frac{{dy}}{{dx}} = 2x + 1 \Rightarrow y = {x^2} + x + k$$

Since, the curve passes through the point $$\left( {1,\,2} \right)$$
$$\eqalign{ & \therefore \,2 = 1 + 1 + k \Rightarrow k = 0 \cr & \therefore \,{\text{The curve is }}y = {x^2} + x \cr} $$
So, the required area
$$\eqalign{ & = \int_0^1 {\left( {{x^2} + x} \right)dx} \cr & = \left[ {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right]_0^1 \cr & = \frac{1}{3} + \frac{1}{2} \cr & = \frac{5}{6}{\text{ sq}}{\text{. unit}} \cr} $$