Question
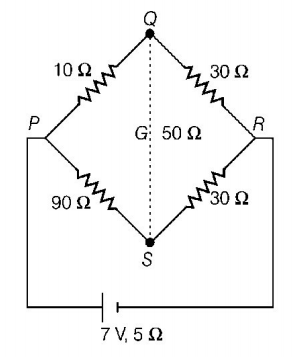
The resistances of the four arms $$P,Q,R$$ and $$S$$ in a Wheatstone bridge are $$10\,\Omega ,30\,\Omega ,30\,\Omega $$ and $$90\,\Omega ,$$ respectively. The emf and internal resistance of the cell are $$7\,V$$ and $$5\,\Omega $$ respectively. If the galvanometer resistance is $$50\,\Omega ,$$ the current drawn from the cell will be
A.
$$1.0\,A$$
B.
$$0.2\,A$$
C.
$$0.1\,A$$
D.
$$2.0\,A$$
Answer :
$$0.2\,A$$
Solution :
Effective resistance,
$$\eqalign{ & \frac{1}{{{R_{{\text{eff}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\,.......\left( {\text{i}} \right) \cr & {\text{then,}}\,\,{R_1} = 10 + 30 \cr & {R_1} = 40 \cr & {\text{Now,}}\,\,{R_2} = 90 + 30 = 120 \cr & {R_2} = 120 \cr} $$
By Eq. (i),
$$\eqalign{ & \frac{1}{{{R_{{\text{eff}}}}}} = \frac{1}{{40}} + \frac{1}{{120}} \cr & {R_{{\text{eff}}}} = \frac{{40 \times 120}}{{120 + 40}} = \frac{{4800}}{{160}} = 30\,\Omega \cr} $$
In the balancing condition,
$$\therefore {\text{Current,}}\,\,I = \frac{7}{{\left( {30 + 5} \right)}} = \frac{7}{{35}} = 0.2\,A\,\,\left[ {\because I = \frac{E}{{R + r}}} \right]$$
Effective resistance,

$$\eqalign{ & \frac{1}{{{R_{{\text{eff}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\,.......\left( {\text{i}} \right) \cr & {\text{then,}}\,\,{R_1} = 10 + 30 \cr & {R_1} = 40 \cr & {\text{Now,}}\,\,{R_2} = 90 + 30 = 120 \cr & {R_2} = 120 \cr} $$
By Eq. (i),
$$\eqalign{ & \frac{1}{{{R_{{\text{eff}}}}}} = \frac{1}{{40}} + \frac{1}{{120}} \cr & {R_{{\text{eff}}}} = \frac{{40 \times 120}}{{120 + 40}} = \frac{{4800}}{{160}} = 30\,\Omega \cr} $$
In the balancing condition,
$$\therefore {\text{Current,}}\,\,I = \frac{7}{{\left( {30 + 5} \right)}} = \frac{7}{{35}} = 0.2\,A\,\,\left[ {\because I = \frac{E}{{R + r}}} \right]$$
