Question
The range of the function $$f\left( x \right) = \left| {x - 1} \right| + \left| {x - 2} \right|,\, - 1 \leqslant x \leqslant 3,$$ is :
A.
$$\left[ {1,\,3} \right]$$
B.
$$\left[ {1,\,5} \right]$$
C.
$$\left[ {3,\,5} \right]$$
D.
none of these
Answer :
$$\left[ {1,\,5} \right]$$
Solution :
If $$x < 1,\,f\left( x \right) = - \left( {x - 1} \right) - \left( {x - 2} \right) = - 2x + 3.$$ In this interval, $$f\left( x \right)$$ is decreasing.
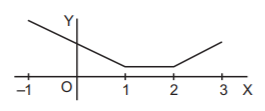
If $$1 \leqslant x < 2,\,f\left( x \right) = x - 1 - \left( {x - 2} \right) = 1$$
In this interval, $$f\left( x \right)$$ is constant.
If $$2 \leqslant x \leqslant 3,\,f\left( x \right) = x - 1 + x - 2 = 2x - 3$$
In this interval, $$f\left( x \right)$$ is increasing.
$$\therefore \max \,f\left( x \right) = $$ the greatest among $$f\left( { - 1} \right)$$ and $$f\left( 3 \right) = 5,\,\,\min \,f\left( x \right) = f\left( 1 \right) = 1$$
So, range $$ = \left[ {1,\,5} \right].$$
If $$x < 1,\,f\left( x \right) = - \left( {x - 1} \right) - \left( {x - 2} \right) = - 2x + 3.$$ In this interval, $$f\left( x \right)$$ is decreasing.

If $$1 \leqslant x < 2,\,f\left( x \right) = x - 1 - \left( {x - 2} \right) = 1$$
In this interval, $$f\left( x \right)$$ is constant.
If $$2 \leqslant x \leqslant 3,\,f\left( x \right) = x - 1 + x - 2 = 2x - 3$$
In this interval, $$f\left( x \right)$$ is increasing.
$$\therefore \max \,f\left( x \right) = $$ the greatest among $$f\left( { - 1} \right)$$ and $$f\left( 3 \right) = 5,\,\,\min \,f\left( x \right) = f\left( 1 \right) = 1$$
So, range $$ = \left[ {1,\,5} \right].$$