Releted MCQ Question on
Modern Physics >> Modern Physics Miscellaneous
Releted Question 1
The maximum kinetic energy of photoelectrons emitted from a surface when photons of energy $$6\,eV$$ fall on it is $$4\,eV.$$ The stopping potential, in volt, is
A.
2
B.
4
C.
6
D.
10
Releted Question 2
Electrons with energy $$80\,keV$$ are incident on the tungsten target of an X-ray tube. $$K$$-shell electrons of tungsten have $$72.5\,keV$$ energy. X-rays emitted by the tube contain only
A.
a continuous X-ray spectrum (Bremsstrahlung) with a
minimum wavelength of $$0.155\mathop {\text{A}}\limits^ \circ $$
B.
a continuous X-ray spectrum (Bremsstrahlung) with all wavelengths
C.
the characteristic X-ray spectrum of tungsten
D.
a continuous X-ray spectrum (Bremsstrahlung) with a
minimum wavelength of $$0.155\mathop {\text{A}}\limits^ \circ $$ and the characteristic X-ray spectrum of tungsten.
Releted Question 3
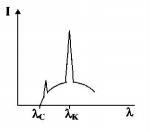
The intensity of X-rays from a Coolidge tube is plotted
against wavelength $$\lambda $$ as shown in the figure. The minimum wavelength found is $${\lambda _C}$$ and the wavelength of the $${K_\alpha }$$ line is $${\lambda _K}.$$ As the accelerating voltage is increased
The intensity of X-rays from a Coolidge tube is plotted
against wavelength $$\lambda $$ as shown in the figure. The minimum wavelength found is $${\lambda _C}$$ and the wavelength of the $${K_\alpha }$$ line is $${\lambda _K}.$$ As the accelerating voltage is increased
A.
$${\lambda _K} - {\lambda _C}$$ increases
B.
$${\lambda _K} - {\lambda _C}$$ decreases
C.
$${\lambda _K}$$ increases
D.
$${\lambda _K}$$ decreases
Releted Question 4
The potential difference applied to an X-ray tube is $$5k\,V$$ and the current through it is 3.2$$mA.$$ Then the number of electrons striking the target per second is
A.
$$2 \times {10^{16}}$$
B.
$$5 \times {10^{6}}$$
C.
$$1 \times {10^{17}}$$
D.
$$4 \times {10^{15}}$$