Question
The point $$P$$ moves in the plane of a regular hexagon such that the sum of the squares of its distances from the vertices of the hexagon is $$6{a^2}.$$ If the radius of the circumcircle of the hexagon is $$r\left( { < a} \right)$$ then the locus of $$P$$ is :
A.
a pair of straight lines
B.
an ellipse
C.
a circle of radius $$\sqrt {{a^2} - {r^2}} $$
D.
an ellipse of major axis $$a$$ and minor axis $$r$$
Answer :
a circle of radius $$\sqrt {{a^2} - {r^2}} $$
Solution :
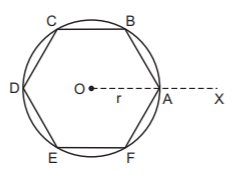
The vertices are $$A\left( {r,\,0} \right),\,B\left( {r\cos \,{{60}^ \circ },\,r\sin \,{{60}^ \circ }} \right),\,C\left( { - r\cos \,{{60}^ \circ },\,r\sin \,{{60}^ \circ }} \right),\,D\left( { - r,\,0} \right),\,E\left( { - r\cos \,{{60}^ \circ },\, - r\sin \,{{60}^ \circ }} \right),\,F\left( {r\cos \,{{60}^ \circ },\, - r\sin \,{{60}^ \circ }} \right).$$
If $$P = \left( {x,\,y} \right)$$ then $$\sum {P{A^2} = 6{a^2}} $$ implies
$$\eqalign{ & \left\{ {{{\left( {x - r} \right)}^2} + {y^2}} \right\} + \left\{ {{{\left( {x - \frac{r}{2}} \right)}^2} + {{\left( {y - \frac{{r\sqrt 3 }}{2}} \right)}^2}} \right\} + ..... + \left\{ {{{\left( {x - \frac{r}{2}} \right)}^2} + {{\left( {x + \frac{{r\sqrt 3 }}{2}} \right)}^2}} \right\} = 6{a^2} \cr & {\text{or }}2\left( {{x^2} + {y^2} + {r^2}} \right) + 2\left( {{x^2} + {y^2} + \frac{{{r^2}}}{4} + \frac{{3{r^2}}}{4}} \right) + 2\left( {{x^2} + {y^2} + \frac{{{r^2}}}{4} + \frac{{3{r^2}}}{4}} \right) = 6{a^2} \cr & {\text{or }}{x^2} + {y^2} + {r^2} = {a^2} \cr & {\text{or }}{x^2} + {y^2} = {\left( {\sqrt {{a^2} - {r^2}} } \right)^2} \cr} $$

The vertices are $$A\left( {r,\,0} \right),\,B\left( {r\cos \,{{60}^ \circ },\,r\sin \,{{60}^ \circ }} \right),\,C\left( { - r\cos \,{{60}^ \circ },\,r\sin \,{{60}^ \circ }} \right),\,D\left( { - r,\,0} \right),\,E\left( { - r\cos \,{{60}^ \circ },\, - r\sin \,{{60}^ \circ }} \right),\,F\left( {r\cos \,{{60}^ \circ },\, - r\sin \,{{60}^ \circ }} \right).$$
If $$P = \left( {x,\,y} \right)$$ then $$\sum {P{A^2} = 6{a^2}} $$ implies
$$\eqalign{ & \left\{ {{{\left( {x - r} \right)}^2} + {y^2}} \right\} + \left\{ {{{\left( {x - \frac{r}{2}} \right)}^2} + {{\left( {y - \frac{{r\sqrt 3 }}{2}} \right)}^2}} \right\} + ..... + \left\{ {{{\left( {x - \frac{r}{2}} \right)}^2} + {{\left( {x + \frac{{r\sqrt 3 }}{2}} \right)}^2}} \right\} = 6{a^2} \cr & {\text{or }}2\left( {{x^2} + {y^2} + {r^2}} \right) + 2\left( {{x^2} + {y^2} + \frac{{{r^2}}}{4} + \frac{{3{r^2}}}{4}} \right) + 2\left( {{x^2} + {y^2} + \frac{{{r^2}}}{4} + \frac{{3{r^2}}}{4}} \right) = 6{a^2} \cr & {\text{or }}{x^2} + {y^2} + {r^2} = {a^2} \cr & {\text{or }}{x^2} + {y^2} = {\left( {\sqrt {{a^2} - {r^2}} } \right)^2} \cr} $$