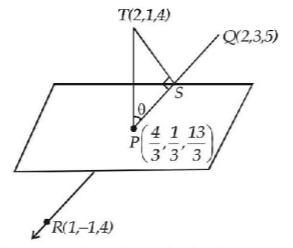
The point $$P$$ is the intersection of the straight line joining the points $$Q\left( {2,\,3,\,5} \right)$$   and $$R\left( {1,\, - 1,\,4} \right)$$   with the plane $$5x-4y-z=1.$$    If $$S$$ is the foot of the perpendicular drawn from the point $$T\left( {2,\,1,\,4} \right)$$   to $$QR,$$  then the length of the line segment $$PS$$ is :

Solution :
Equation of straight line joining $$Q\left( {2,\,3,\,5} \right)$$   and $$R\left( {1,\, - 1,\,4} \right)$$   is
$$\eqalign{ & \frac{{x - 2}}{{ - 1}} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 5}}{1} = \lambda \cr & {\text{Let }}P\left( { - \lambda + 2,\, - 4\lambda + 3,\, - \lambda + 5} \right) \cr} $$
As $$P$$ lies on $$5x-4y-z=1$$
$$\eqalign{ & \therefore - 5\lambda + 10 + 16\lambda - 12 + \lambda - 5 = 1 \cr & \Rightarrow 12\lambda = 8 \cr & \Rightarrow \lambda = \frac{2}{3} \cr & \therefore P = \left( {\frac{4}{3},\,\frac{1}{3},\,\frac{{13}}{3}} \right) \cr} $$
Now let point $$S$$ on $$QR$$  be
$$\left( { - \mu + 2,\, - 4\mu + 3,\, - \mu + 5} \right)$$
$$\because \,S$$  is the foot of perpendicular drawn from $$T\left( {2,\,1,\,4} \right)$$   to $$QR,$$  where dr’s of $$ST$$  are $$\mu ,\,4\mu - 2,\,\mu - 1$$   and dr’s of $$QR$$ are $$-1,\,-4,\,-1$$
$$\eqalign{ & \therefore - \mu - 16\mu + 8 - \mu + 1 = 0 \cr & \Rightarrow 18\mu = 9 \cr & \Rightarrow \mu = \frac{1}{2} \cr & \therefore S = \left( {\frac{3}{2},\,1,\,\frac{9}{2}} \right) \cr} $$
$$\therefore $$ Distance between $$P$$ and $$S$$
$$\eqalign{ & = \sqrt {{{\left( {\frac{4}{3} - \,\frac{3}{2}} \right)}^2} + {{\left( {\frac{1}{3} - 1} \right)}^2} + {{\left( {\frac{{13}}{3} - \frac{9}{2}} \right)}^2}} \cr & = \sqrt {\frac{1}{{36}} + \frac{4}{9} + \frac{1}{{36}}} \cr & = \frac{1}{{\sqrt 2 }} \cr} $$