Question
The point diametrically opposite to the point $$P\left( {1,\,0} \right)$$ on the circle $${x^2} + {y^2} + 2x + 4y - 3 = 0$$ is-
A.
$$\left( {3,\, - 4} \right)$$
B.
$$\left( { - 3,\,4} \right)$$
C.
$$\left( { - 3,\, - 4} \right)$$
D.
$$\left( {3,\,4} \right)$$
Answer :
$$\left( { - 3,\, - 4} \right)$$
Solution :
The given circle is $${x^2} + {y^2} + 2x + 4y - 3 = 0$$
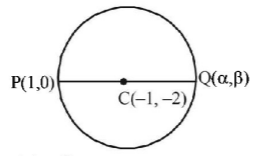
Centre $$\left( { - 1,\, - 2} \right)$$
Let $$Q\left( {\alpha ,\,\beta } \right)$$ be the point diametrically opposite to the point $$P\left( {1,\,0} \right),$$
then $$\frac{{1 + \alpha }}{2} = - 1{\text{ and }}\frac{{0 + \beta }}{2} = - 2$$
$$ \Rightarrow \alpha = - 3,\,\,\beta = - 4,\,\,\,{\text{So }}Q\,\,{\text{is}}\left( { - 3,\, - 4} \right)$$
The given circle is $${x^2} + {y^2} + 2x + 4y - 3 = 0$$

Centre $$\left( { - 1,\, - 2} \right)$$
Let $$Q\left( {\alpha ,\,\beta } \right)$$ be the point diametrically opposite to the point $$P\left( {1,\,0} \right),$$
then $$\frac{{1 + \alpha }}{2} = - 1{\text{ and }}\frac{{0 + \beta }}{2} = - 2$$
$$ \Rightarrow \alpha = - 3,\,\,\beta = - 4,\,\,\,{\text{So }}Q\,\,{\text{is}}\left( { - 3,\, - 4} \right)$$