Question
The point $$\left( {a,\,2a} \right)$$ is an interior point of the region bounded by the parabola $${y^2} = 16x$$ and the double ordinate through the focus. Then $$a$$ belongs to the open interval :
A.
$$a < 4$$
B.
$$0 < a < 4$$
C.
$$0 < a < 2$$
D.
$$a > 4$$
Answer :
$$0 < a < 4$$
Solution :
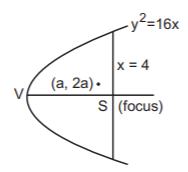
$$\left( {a,\,2a} \right)$$ is an interior point of $${y^2} - 16x = 0$$ if $${\left( {2a} \right)^2} - 16a < 0,$$ i.e., $${a^2} - 4a < 0$$
$$V\left( {0,\,0} \right)$$ and $$\left( {a,\,2a} \right)$$ are on the same side of $$x - 4 = 0.$$ So, $$a - 4 < 0,$$ i.e., $$a < 4$$
Now, $${a^2} - 4a < 0\,\,\,\,\,\, \Rightarrow 0 < a < 4$$

$$\left( {a,\,2a} \right)$$ is an interior point of $${y^2} - 16x = 0$$ if $${\left( {2a} \right)^2} - 16a < 0,$$ i.e., $${a^2} - 4a < 0$$
$$V\left( {0,\,0} \right)$$ and $$\left( {a,\,2a} \right)$$ are on the same side of $$x - 4 = 0.$$ So, $$a - 4 < 0,$$ i.e., $$a < 4$$
Now, $${a^2} - 4a < 0\,\,\,\,\,\, \Rightarrow 0 < a < 4$$