Question
The point (4, 1) undergoes the following three transformations successively.
The point (4, 1) undergoes the following three transformations successively.
(i) Reflection about the line $$y =x.$$
(ii) Translation through a distance 2 units along the positive direction of $$x$$-axis.
(iii) Rotation through an angle $$\frac{p}{4}$$ about the origin in the counter clockwise direction.
Then the final position of the point is given by the coordinates.
A.
$$\left( {\frac{1}{{\sqrt 2 }},\,\frac{7}{{\sqrt 2 }}} \right)$$
B.
$$\left( { - \sqrt 2 ,\,7\sqrt 2 } \right)$$
C.
$$\left( { - \frac{1}{{\sqrt 2 }},\,\frac{7}{{\sqrt 2 }}} \right)$$
D.
$$\left( {\sqrt 2 ,\,7\sqrt 2 } \right)$$
Answer :
$$\left( { - \frac{1}{{\sqrt 2 }},\,\frac{7}{{\sqrt 2 }}} \right)$$
Solution :
Reflection about the line $$y =x,$$ changes the point (4, 1) to (1, 4).
On translation of (1, 4) through a distance of 2 units along $$+ve$$ direction of $$x$$-axis the point becomes (1 + 2, 4), i.e., (3, 4).
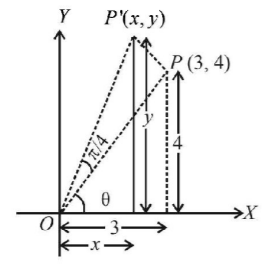
On rotation about origin through an angle $$\frac{\pi }{4}$$ the point $$P$$ takes the position $$P'$$ such that
$$OP= OP'$$
Also $$OP = 5 = OP'$$ and $$\cos \,\theta = \frac{3}{5},\,\,\,\sin \,\theta = \frac{4}{5}$$
$$\eqalign{ & {\text{Now, }}\,x = OP'\cos \left( {\frac{\pi }{4} + \theta } \right) \cr & = 5\left( {\cos \frac{\pi }{4}\cos \,\theta - \sin \frac{\pi }{4}\sin \,\theta } \right) \cr & = 5\left( {\frac{3}{{5\sqrt 2 }} - \frac{4}{{5\sqrt 2 }}} \right) \cr & = - \frac{1}{{\sqrt 2 }} \cr & y = OP'\sin \left( {\frac{\pi }{4} + \theta } \right) \cr & = 5\left( {\sin \frac{\pi }{4}\cos \,\theta + \cos \frac{\pi }{4}\sin \,\theta } \right) \cr & = 5\left( {\frac{3}{{5\sqrt 2 }} + \frac{4}{{5\sqrt 2 }}} \right) \cr & = \frac{7}{{\sqrt 2 }} \cr & \therefore P' = \left( { - \frac{1}{{\sqrt 2 }},\,\frac{7}{{\sqrt 2 }}} \right) \cr} $$
Reflection about the line $$y =x,$$ changes the point (4, 1) to (1, 4).
On translation of (1, 4) through a distance of 2 units along $$+ve$$ direction of $$x$$-axis the point becomes (1 + 2, 4), i.e., (3, 4).

On rotation about origin through an angle $$\frac{\pi }{4}$$ the point $$P$$ takes the position $$P'$$ such that
$$OP= OP'$$
Also $$OP = 5 = OP'$$ and $$\cos \,\theta = \frac{3}{5},\,\,\,\sin \,\theta = \frac{4}{5}$$
$$\eqalign{ & {\text{Now, }}\,x = OP'\cos \left( {\frac{\pi }{4} + \theta } \right) \cr & = 5\left( {\cos \frac{\pi }{4}\cos \,\theta - \sin \frac{\pi }{4}\sin \,\theta } \right) \cr & = 5\left( {\frac{3}{{5\sqrt 2 }} - \frac{4}{{5\sqrt 2 }}} \right) \cr & = - \frac{1}{{\sqrt 2 }} \cr & y = OP'\sin \left( {\frac{\pi }{4} + \theta } \right) \cr & = 5\left( {\sin \frac{\pi }{4}\cos \,\theta + \cos \frac{\pi }{4}\sin \,\theta } \right) \cr & = 5\left( {\frac{3}{{5\sqrt 2 }} + \frac{4}{{5\sqrt 2 }}} \right) \cr & = \frac{7}{{\sqrt 2 }} \cr & \therefore P' = \left( { - \frac{1}{{\sqrt 2 }},\,\frac{7}{{\sqrt 2 }}} \right) \cr} $$