Question
The particle executing simple harmonic motion has a kinetic energy $${K_0}{\cos ^2}\omega t.$$ The maximum values of the potential energy and the total energy are respectively
A.
$$0\,\,{\text{and}}\,\,2{K_0}$$
B.
$$\frac{{{K_0}}}{2}\,\,{\text{and}}\,\,{K_0}$$
C.
$${K_0}\,\,{\text{and}}\,\,2{K_0}$$
D.
$${K_0}\,\,{\text{and}}\,\,{K_0}$$
Answer :
$${K_0}\,\,{\text{and}}\,\,{K_0}$$
Solution :
In simple harmonic motion, the total energy of the particle is constant at all instants which is totally kinetic when particle is passing through the mean position and is totally potential when particle is passing through the extreme position.
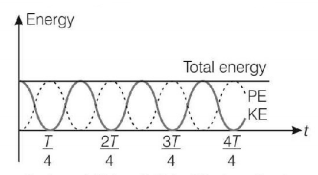
The variation of $$PE$$ and $$KE$$ with time is shown in figure, by dotted parabolic curve and solid parabolic curve respectively.
Figure indicates that maximum values of total energy, $$KE$$ and $$PE$$ of $$SHM$$ are equal.
$$\eqalign{ & {\text{Now,}}\,\,KE = {K_0}{\cos ^2}\omega t \cr & \therefore K{E_{\max }} = {K_0} \cr & {\text{So,}}\,P{E_{\max }} = {K_0} \cr & {\text{and}}\,\,{\left( E \right)_{{\text{Total}}}} = {K_0} \cr} $$
In simple harmonic motion, the total energy of the particle is constant at all instants which is totally kinetic when particle is passing through the mean position and is totally potential when particle is passing through the extreme position.

The variation of $$PE$$ and $$KE$$ with time is shown in figure, by dotted parabolic curve and solid parabolic curve respectively.
Figure indicates that maximum values of total energy, $$KE$$ and $$PE$$ of $$SHM$$ are equal.
$$\eqalign{ & {\text{Now,}}\,\,KE = {K_0}{\cos ^2}\omega t \cr & \therefore K{E_{\max }} = {K_0} \cr & {\text{So,}}\,P{E_{\max }} = {K_0} \cr & {\text{and}}\,\,{\left( E \right)_{{\text{Total}}}} = {K_0} \cr} $$