Question
The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is
The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is

A.
$$2!\, \times 2!$$
B.
$$4!$$
C.
$$2\left( {4!} \right)$$
D.
None of these
Answer :
None of these
Solution :
The natural numbers are 1, 2, 3, 4.
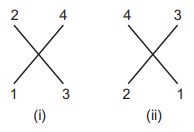
Clearly, in one diagonal we have to place 1, 4 and in the other 2, 3.
The number of ways in (i) $$ = 2!\, \times 2! = 4.$$
The number of ways in (ii) $$ = 2!\, \times 2! = 4.$$
∴ the total number of ways = 8.
The natural numbers are 1, 2, 3, 4.

Clearly, in one diagonal we have to place 1, 4 and in the other 2, 3.
The number of ways in (i) $$ = 2!\, \times 2! = 4.$$
The number of ways in (ii) $$ = 2!\, \times 2! = 4.$$
∴ the total number of ways = 8.