Question
The number of different ways in which 8 persons can stand in a row so that between two particular persons $$A$$ and $$B$$ there are always two persons, is
A.
$$60\left( {5!} \right)$$
B.
$$15\left( {4!} \right) \times \left( {5!} \right)$$
C.
$$4!\, \times 5!$$
D.
None of these
Answer :
$$60\left( {5!} \right)$$
Solution :
The number of selections of 4 persons including $$A,B = {\,^6}{C_2}.$$
Considering these four as a group, number of arrangements with the other four $$= 5!.$$
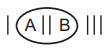
But in each group the number of arrangements $$ = 2!\, \times 2!$$
∴ the required number of ways $$ = {\,^6}{C_2} \times 5!\, \times 2!\, \times 2!.$$
The number of selections of 4 persons including $$A,B = {\,^6}{C_2}.$$
Considering these four as a group, number of arrangements with the other four $$= 5!.$$
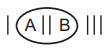
But in each group the number of arrangements $$ = 2!\, \times 2!$$
∴ the required number of ways $$ = {\,^6}{C_2} \times 5!\, \times 2!\, \times 2!.$$