Question
The number of common tangents to the circles $${x^2} + {y^2} - 4x - 6y - 12 = 0$$ and $${x^2} + {y^2} + 6x + 18y + 26 = 0$$ is :
A.
$$3$$
B.
$$4$$
C.
$$1$$
D.
$$2$$
Answer :
$$3$$
Solution :
$${x^2} + {y^2} - 4x - 6y - 12 = 0.....({\text{i}})$$
Centre, $${c_1} = \left( {2,\,3} \right)$$ and Radius, $${r_1} = 5\,{\text{units}}$$
$${x^2} + {y^2} + 6x + 18y + 26 = 0.....({\text{ii}})$$
Centre, $${c_2} = \left( { - 3,\, - 9} \right)$$ and Radius, $${r_2} = 8\,{\text{units}}$$
$$\eqalign{ & {C_1}{C_2} = \sqrt {{{\left( {2 + 3} \right)}^2} + {{\left( {3 + 9} \right)}^2}} = 13\,{\text{units}} \cr & {r_1} + {r_2} = 5 + 8 = 13 \cr & \therefore {C_1}{C_2} = {r_1} + {r_2} \cr} $$
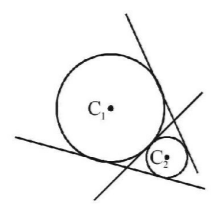
Therefore there are three common tangents.
$${x^2} + {y^2} - 4x - 6y - 12 = 0.....({\text{i}})$$
Centre, $${c_1} = \left( {2,\,3} \right)$$ and Radius, $${r_1} = 5\,{\text{units}}$$
$${x^2} + {y^2} + 6x + 18y + 26 = 0.....({\text{ii}})$$
Centre, $${c_2} = \left( { - 3,\, - 9} \right)$$ and Radius, $${r_2} = 8\,{\text{units}}$$
$$\eqalign{ & {C_1}{C_2} = \sqrt {{{\left( {2 + 3} \right)}^2} + {{\left( {3 + 9} \right)}^2}} = 13\,{\text{units}} \cr & {r_1} + {r_2} = 5 + 8 = 13 \cr & \therefore {C_1}{C_2} = {r_1} + {r_2} \cr} $$

Therefore there are three common tangents.