Question
The minimum value of $$\left| z \right| + \left| {z - i} \right|$$ is
A.
0
B.
1
C.
2
D.
None of these
Answer :
1
Solution :
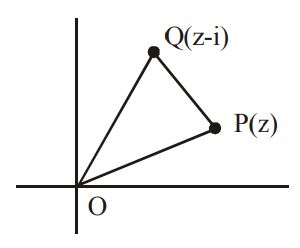
Using the result $$\left| {{z_1} + {z_2}} \right| \leqslant \left| {{z_1}} \right| + \left| {{z_2}} \right|,$$
we get, $$\left| z \right| + \left| {z - i} \right| = \left| z \right| + \left| {i - z} \right|\,\,\,\,\left[ {{\text{since}}\,\left| z \right| = \left| { - z} \right|} \right]$$
$$ \leqslant \left| {z + i - z} \right| = \left| i \right| = 1$$
∴ minimum value of $$\left| z \right| + \left| {z - i} \right|\,\,{\text{is}}\,\,1$$

Using the result $$\left| {{z_1} + {z_2}} \right| \leqslant \left| {{z_1}} \right| + \left| {{z_2}} \right|,$$
we get, $$\left| z \right| + \left| {z - i} \right| = \left| z \right| + \left| {i - z} \right|\,\,\,\,\left[ {{\text{since}}\,\left| z \right| = \left| { - z} \right|} \right]$$
$$ \leqslant \left| {z + i - z} \right| = \left| i \right| = 1$$
∴ minimum value of $$\left| z \right| + \left| {z - i} \right|\,\,{\text{is}}\,\,1$$