Question
The minimum area of triangle formed by the tangent to the $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ & coordinate axes is-
A.
$$ab\,\,{\text{sq}}{\text{. units}}$$
B.
$$\frac{{{a^2} + {b^2}}}{2}\,\,{\text{sq}}{\text{. units}}$$
C.
$$\frac{{{{\left( {a + b} \right)}^2}}}{2}\,\,{\text{sq}}{\text{. units}}$$
D.
$$\frac{{{a^2} + ab + {b^2}}}{3}\,\,{\text{sq}}{\text{. units}}$$
Answer :
$$ab\,\,{\text{sq}}{\text{. units}}$$
Solution :
Any tangent to the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ at $$P\left( {a\,\cos \,\theta ,\,b\,\sin \,\theta } \right)$$ is $$\frac{{x\,\cos \,\theta }}{a} + \frac{{y\,\sin \,\theta }}{b} = 1$$
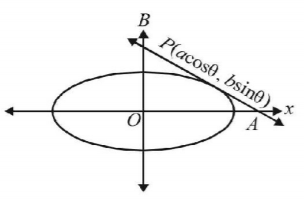
It meets co-ordinate axes at $$A\left( {a\,\sec \,\theta ,\,0} \right)$$ and $$B\left( {0,\,b\,{\text{cosec}}\,\theta } \right)$$
$$\therefore $$ Area of $$\Delta OAB = \frac{1}{2} \times a\,\sec \,\theta \times b\,{\text{cosec}}\,\theta $$
$$ \Rightarrow \Delta = \frac{{ab}}{{\sin \,2\theta }}$$
For $$\Delta $$ to be min, $${\sin \,2\theta }$$ should be max. and we know max. value of $$\sin \,2\theta = 1$$
$$\therefore {\Delta _{\max }} = ab\,\,{\text{sq}}{\text{. units}}$$
Any tangent to the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ at $$P\left( {a\,\cos \,\theta ,\,b\,\sin \,\theta } \right)$$ is $$\frac{{x\,\cos \,\theta }}{a} + \frac{{y\,\sin \,\theta }}{b} = 1$$

It meets co-ordinate axes at $$A\left( {a\,\sec \,\theta ,\,0} \right)$$ and $$B\left( {0,\,b\,{\text{cosec}}\,\theta } \right)$$
$$\therefore $$ Area of $$\Delta OAB = \frac{1}{2} \times a\,\sec \,\theta \times b\,{\text{cosec}}\,\theta $$
$$ \Rightarrow \Delta = \frac{{ab}}{{\sin \,2\theta }}$$
For $$\Delta $$ to be min, $${\sin \,2\theta }$$ should be max. and we know max. value of $$\sin \,2\theta = 1$$
$$\therefore {\Delta _{\max }} = ab\,\,{\text{sq}}{\text{. units}}$$