Question
The mass of a hydrogen molecule is $$3.32 \times {10^{ - 27}}\,kg.$$ If $${10^{23}}$$ hydrogen molecules strike, per second, a fixed wall of area $$2\,c{m^2}$$ at an angle of 45° to the normal, and rebound elastically with a speed of $${10^3}\,m/s,$$ then the pressure on the wall is nearly :
A.
$$2.35 \times {10^3}\,N/{m^2}$$
B.
$$4.70 \times {10^3}\,N/{m^2}$$
C.
$$2.35 \times {10^2}\,N/{m^2}$$
D.
$$4.70 \times {10^2}\,N/{m^2}$$
Answer :
$$2.35 \times {10^3}\,N/{m^2}$$
Solution :
Change in momentum
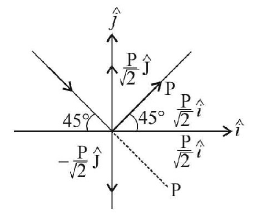
$$\eqalign{ & \Delta P = \frac{P}{{\sqrt 2 }}\hat J + \frac{P}{{\sqrt 2 }}\hat J + \frac{P}{{\sqrt 2 }}\hat i - \frac{P}{{\sqrt 2 }}\hat i \cr & \Delta P = \frac{{2P}}{{\sqrt 2 }}\hat J = {I_H}\,\,{\text{molecule}} \cr & \Rightarrow \,\,{I_{{\text{wall}}}} = - \frac{{2P}}{{\sqrt 2 }}\hat J \cr & {\text{Pressure, }}P \cr & = \frac{F}{A} = \frac{{\sqrt 2 P}}{A}n\,\,\left( {\because \,n = {\text{no}}{\text{. of particles}}} \right) \cr & = \frac{{\sqrt 2 \times 3.32 \times {{10}^{ - 27}} \times {{10}^3} \times {{10}^{23}}}}{{2 \times {{10}^{ - 4}}}} \cr & = 2.35 \times {10^3}\,N/{m^2} \cr} $$
Change in momentum

$$\eqalign{ & \Delta P = \frac{P}{{\sqrt 2 }}\hat J + \frac{P}{{\sqrt 2 }}\hat J + \frac{P}{{\sqrt 2 }}\hat i - \frac{P}{{\sqrt 2 }}\hat i \cr & \Delta P = \frac{{2P}}{{\sqrt 2 }}\hat J = {I_H}\,\,{\text{molecule}} \cr & \Rightarrow \,\,{I_{{\text{wall}}}} = - \frac{{2P}}{{\sqrt 2 }}\hat J \cr & {\text{Pressure, }}P \cr & = \frac{F}{A} = \frac{{\sqrt 2 P}}{A}n\,\,\left( {\because \,n = {\text{no}}{\text{. of particles}}} \right) \cr & = \frac{{\sqrt 2 \times 3.32 \times {{10}^{ - 27}} \times {{10}^3} \times {{10}^{23}}}}{{2 \times {{10}^{ - 4}}}} \cr & = 2.35 \times {10^3}\,N/{m^2} \cr} $$
