Question
The locus of $$z$$ which lies in shaded region (excluding the boundaries) is best represented by
The locus of $$z$$ which lies in shaded region (excluding the boundaries) is best represented by
A.
$$z:\left| {z + 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}$$
B.
$$z:\left| {z - 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z - 1} \right)} \right| < \frac{\pi }{4}$$
C.
$$z:\left| {z + 1} \right| < 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{2}$$
D.
$$z:\left| {z - 1} \right| < 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{2}$$
Answer :
$$z:\left| {z + 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}$$
Solution :
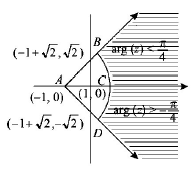
Here we observe that.
$$AB = AC = AD = 2$$
∴ $$BCD$$ is an arc of a circle with center at $$A$$ and radius 2. Shaded region is outer (exterior) part of this sector $$ABCDA.$$
∴ For any pt. $$z$$ on are $$BCD$$ we should have
$$\left| {z - \left( { - 1} \right)} \right| = 2$$
and for shaded region, $$\left| {z + 1} \right| > 2\,\,\,\,\,\,\,\,......\left( {\text{i}} \right)$$
For shaded region we also have
$$\eqalign{ & - \frac{\pi }{4} < \arg \left( {z + 1} \right) < \frac{\pi }{4} \cr & {\text{or }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}\,\,\,\,\,\,\,\,\,\,......\left( {{\text{ii}}} \right) \cr} $$
Combining (i) and (ii), (A) is the correct option.
Here we observe that.
$$AB = AC = AD = 2$$
∴ $$BCD$$ is an arc of a circle with center at $$A$$ and radius 2. Shaded region is outer (exterior) part of this sector $$ABCDA.$$
∴ For any pt. $$z$$ on are $$BCD$$ we should have
$$\left| {z - \left( { - 1} \right)} \right| = 2$$
and for shaded region, $$\left| {z + 1} \right| > 2\,\,\,\,\,\,\,\,......\left( {\text{i}} \right)$$
For shaded region we also have
$$\eqalign{ & - \frac{\pi }{4} < \arg \left( {z + 1} \right) < \frac{\pi }{4} \cr & {\text{or }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}\,\,\,\,\,\,\,\,\,\,......\left( {{\text{ii}}} \right) \cr} $$
Combining (i) and (ii), (A) is the correct option.