Question
The locus of the point of intersection of two tangents to the parabola $${y^2} = 4ax,$$ which are at right angle to one another is :
A.
$${x^2} + {y^2} = {a^2}$$
B.
$$a{y^2} = x$$
C.
$$x + a = 0$$
D.
$$x + y \pm a = 0$$
Answer :
$$x + a = 0$$
Solution :
Let the two tangents to the parabola $${y^2} = 4ax$$ be $$PT$$ and $$QT$$ which are at right angle to one another at $$T\left( {h,\,k} \right).$$ Then we have to find the locus of $$T\left( {h,\,k} \right).$$
We know that $$y = mx + \frac{a}{m},$$ where $$m$$ is the slope is the equation of tangent to the parabola $${y^2} = 4ax$$ for all $$m.$$
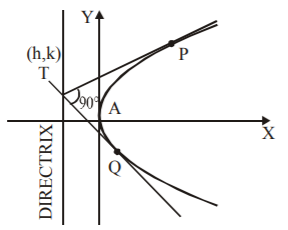
Since this tangent to the parabola will pass through $$T\left( {h,\,k} \right)$$ so $$k = mh + \frac{a}{m}\,;\,\,{\text{or}}\,{\text{ }}{m^2}h - mk + a = 0$$
This is a quadratic equation in $$m$$ so will have two roots, say $${m_1}$$ and $${m_2},$$ then
$${m_1} + {m_2} = \frac{k}{h},\,\,{\text{and}}\,{\text{ }}{m_1}:{m_2} = \frac{a}{h}$$
Given that the two tangents intersect at right angle so $${m_1}.{m_2} = - 1{\text{ or }}\frac{a}{h} = - 1{\text{ or }}h + a = 0$$
The locus of $$T\left( {h,\,k} \right)$$ is $$x + a = 0,$$ which is the equation of directrix.
Let the two tangents to the parabola $${y^2} = 4ax$$ be $$PT$$ and $$QT$$ which are at right angle to one another at $$T\left( {h,\,k} \right).$$ Then we have to find the locus of $$T\left( {h,\,k} \right).$$
We know that $$y = mx + \frac{a}{m},$$ where $$m$$ is the slope is the equation of tangent to the parabola $${y^2} = 4ax$$ for all $$m.$$

Since this tangent to the parabola will pass through $$T\left( {h,\,k} \right)$$ so $$k = mh + \frac{a}{m}\,;\,\,{\text{or}}\,{\text{ }}{m^2}h - mk + a = 0$$
This is a quadratic equation in $$m$$ so will have two roots, say $${m_1}$$ and $${m_2},$$ then
$${m_1} + {m_2} = \frac{k}{h},\,\,{\text{and}}\,{\text{ }}{m_1}:{m_2} = \frac{a}{h}$$
Given that the two tangents intersect at right angle so $${m_1}.{m_2} = - 1{\text{ or }}\frac{a}{h} = - 1{\text{ or }}h + a = 0$$
The locus of $$T\left( {h,\,k} \right)$$ is $$x + a = 0,$$ which is the equation of directrix.