Question
The line passing through the extremity $$A$$ of the major axis and extremity $$B$$ of the minor axis of the ellipse $${x^2} + 9{y^2} = 9$$ meets its auxiliary circle at the point $$M.$$ Then the area of the triangle with vertices at $$A,\,M$$ and the origin $$O$$ is-
A.
$$\frac{{31}}{{10}}$$
B.
$$\frac{{29}}{{10}}$$
C.
$$\frac{{21}}{{10}}$$
D.
$$\frac{{27}}{{10}}$$
Answer :
$$\frac{{27}}{{10}}$$
Solution :
The given ellipse is $${x^2} + 9{y^2} = 9$$ or $$\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{1^2}}} = 1$$
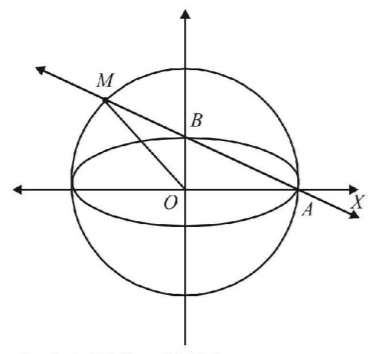
So, that $$A\left( {3,\,0} \right)$$ and $$B\left( {0,\,1} \right)$$
$$\therefore $$ Equation of $$AB$$ is $$\frac{x}{3} + \frac{y}{1} = 1$$
or $$x + 3y - 3 = 0.....(1)$$
Also auxiliary circle of given ellipse is
$${x^2} + {y^2} = 9.....(2)$$
Solving equation (1) and (2), we get the point $$M$$ where line $$AB$$ meets the auxiliary circle.
Putting $$x=3-3y$$ from equation (1) in equation (2)
we get $${\left( {3 - 3y} \right)^2} + {y^2} = 9$$
$$\eqalign{ & \Rightarrow 9 - 18y + 9{y^2} + {y^2} = 9 \cr & \Rightarrow 10{y^2} - 18y = 0 \cr & \Rightarrow y = 0,\,\frac{9}{5}\,\,\,\,\,\,\, \Rightarrow x = 3,\,\frac{{ - 12}}{5} \cr} $$
Clearly $$M\left( {\frac{{ - 12}}{5},\,\frac{9}{5}} \right)$$
$$\therefore $$ Area of \[\Delta OAM = \frac{1}{2}\left| \begin{array}{l} \,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,1\\ \,\,\,3\,\,\,\,\,\,\,\,\,\,0\,\,\,\,1\\ \frac{{ - 12}}{5}\,\,\,\frac{9}{5}\,\,\,1 \end{array} \right| = \frac{{27}}{{10}}\]
The given ellipse is $${x^2} + 9{y^2} = 9$$ or $$\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{1^2}}} = 1$$

So, that $$A\left( {3,\,0} \right)$$ and $$B\left( {0,\,1} \right)$$
$$\therefore $$ Equation of $$AB$$ is $$\frac{x}{3} + \frac{y}{1} = 1$$
or $$x + 3y - 3 = 0.....(1)$$
Also auxiliary circle of given ellipse is
$${x^2} + {y^2} = 9.....(2)$$
Solving equation (1) and (2), we get the point $$M$$ where line $$AB$$ meets the auxiliary circle.
Putting $$x=3-3y$$ from equation (1) in equation (2)
we get $${\left( {3 - 3y} \right)^2} + {y^2} = 9$$
$$\eqalign{ & \Rightarrow 9 - 18y + 9{y^2} + {y^2} = 9 \cr & \Rightarrow 10{y^2} - 18y = 0 \cr & \Rightarrow y = 0,\,\frac{9}{5}\,\,\,\,\,\,\, \Rightarrow x = 3,\,\frac{{ - 12}}{5} \cr} $$
Clearly $$M\left( {\frac{{ - 12}}{5},\,\frac{9}{5}} \right)$$
$$\therefore $$ Area of \[\Delta OAM = \frac{1}{2}\left| \begin{array}{l} \,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,1\\ \,\,\,3\,\,\,\,\,\,\,\,\,\,0\,\,\,\,1\\ \frac{{ - 12}}{5}\,\,\,\frac{9}{5}\,\,\,1 \end{array} \right| = \frac{{27}}{{10}}\]