Question
The length of the perpendicular from the origin to a line is $$7$$ and line makes an angle of $${150^ \circ }$$ with the positive direction of $$y$$-axis, then the equation of the line is :
A.
$$\sqrt 3 \,x + y = 7$$
B.
$$\sqrt 3 \,x - y = 14$$
C.
$$\sqrt 3 \,x + y + 14 = 0$$
D.
$$\sqrt 3 \,x + y - 14 = 0$$
Answer :
$$\sqrt 3 \,x + y - 14 = 0$$
Solution :
Here $$p = 7$$ and $$\alpha = {30^ \circ }$$
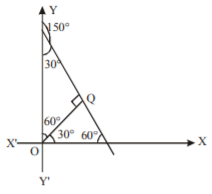
$$\therefore $$ Equation of the required line is
$$\eqalign{ & x\,\cos \,{30^ \circ } + y\,\sin \,{30^ \circ } = 7 \cr & {\text{or }}x \times \frac{{\sqrt 3 }}{2} + y \times \frac{1}{2} = 7 \cr & {\text{or }}\sqrt 3 \,x + y = 14 \cr} $$
Here $$p = 7$$ and $$\alpha = {30^ \circ }$$

$$\therefore $$ Equation of the required line is
$$\eqalign{ & x\,\cos \,{30^ \circ } + y\,\sin \,{30^ \circ } = 7 \cr & {\text{or }}x \times \frac{{\sqrt 3 }}{2} + y \times \frac{1}{2} = 7 \cr & {\text{or }}\sqrt 3 \,x + y = 14 \cr} $$