Question
The length of the diameter of the circle which touches the $$x$$-axis at the point $$\left( {1,\,0} \right)$$ and passes through the point $$\left( {2,\,3} \right)$$ is:
A.
$$\frac{{10}}{3}$$
B.
$$\frac{3}{5}$$
C.
$$\frac{6}{5}$$
D.
$$\frac{5}{3}$$
Answer :
$$\frac{{10}}{3}$$
Solution :
Let centre of the circle be $$\left( {1,\,h} \right)$$ [ $$\because $$ circle touches $$x$$-axis at $$\left( {1,\,0} \right)$$ ]
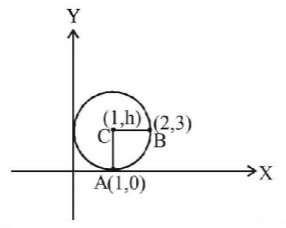
Let the circle passes through the point $$B\left( {2,\,3} \right)$$
$$\eqalign{ & \therefore CA = CB\,\,\,\,\,\,\,\left( {{\text{radius}}} \right) \cr & \Rightarrow C{A^2} = C{B^2} \cr & \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {h - 0} \right)^2} = {\left( {1 - 2} \right)^2} + {\left( {h - 3} \right)^2} \cr & \Rightarrow {h^2} = 1 + {h^2} + 9 - 6h \cr & \Rightarrow h = \frac{{10}}{6} = \frac{5}{3} \cr} $$
Thus, diameter is $$2h = \frac{{10}}{3}$$
Let centre of the circle be $$\left( {1,\,h} \right)$$ [ $$\because $$ circle touches $$x$$-axis at $$\left( {1,\,0} \right)$$ ]

Let the circle passes through the point $$B\left( {2,\,3} \right)$$
$$\eqalign{ & \therefore CA = CB\,\,\,\,\,\,\,\left( {{\text{radius}}} \right) \cr & \Rightarrow C{A^2} = C{B^2} \cr & \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {h - 0} \right)^2} = {\left( {1 - 2} \right)^2} + {\left( {h - 3} \right)^2} \cr & \Rightarrow {h^2} = 1 + {h^2} + 9 - 6h \cr & \Rightarrow h = \frac{{10}}{6} = \frac{5}{3} \cr} $$
Thus, diameter is $$2h = \frac{{10}}{3}$$