Question
The length of a wire of a potentiometer is $$100\,cm,$$ and the e. m.f. of its standard cell is $$E$$ volt. It is employed to measure the e.m.f. of a battery whose internal resistance is $$0.5\,\Omega $$. If the balance point is obtained at $$1 = 30 cm$$ from the positive end, the e.m.f. of the battery is:
The length of a wire of a potentiometer is $$100\,cm,$$ and the e. m.f. of its standard cell is $$E$$ volt. It is employed to measure the e.m.f. of a battery whose internal resistance is $$0.5\,\Omega $$. If the balance point is obtained at $$1 = 30 cm$$ from the positive end, the e.m.f. of the battery is:
(where $$i$$ is the current in the potentiometer wire.)
A.
$$\frac{{30E}}{{100.5}}$$
B.
$$\frac{{30E}}{{\left( {100 - 0.5} \right)}}$$
C.
$$\frac{{30\left( {E - 0.5i} \right)}}{{100}}$$
D.
$$\frac{{30E}}{{100}}$$
Answer :
$$\frac{{30E}}{{100}}$$
Solution :
From the principle of potentiometer, $$V \propto l$$
$$ \Rightarrow \frac{V}{E} = \frac{l}{L};\,{\text{where}}$$
$$V =$$ emf of battery, $$E =$$ emf of standard cell.
$$L =$$ length of potentiometer wire
$$V = \frac{{El}}{L} = \frac{{30E}}{{100}}$$
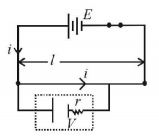
NOTE: In this arrangement, the internal resistance of the battery $$E$$ does not play any role as current is not passing through the battery.
From the principle of potentiometer, $$V \propto l$$
$$ \Rightarrow \frac{V}{E} = \frac{l}{L};\,{\text{where}}$$
$$V =$$ emf of battery, $$E =$$ emf of standard cell.
$$L =$$ length of potentiometer wire
$$V = \frac{{El}}{L} = \frac{{30E}}{{100}}$$

NOTE: In this arrangement, the internal resistance of the battery $$E$$ does not play any role as current is not passing through the battery.
