Question
The intensity of a point source of light, $$S,$$ placed at a distance $$d$$ in front of a screen $$A,$$ is $${I_0}$$ at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror $$M$$ is placed at a distance $$d$$ behind the source, as shown in figure.
The intensity of a point source of light, $$S,$$ placed at a distance $$d$$ in front of a screen $$A,$$ is $${I_0}$$ at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror $$M$$ is placed at a distance $$d$$ behind the source, as shown in figure.
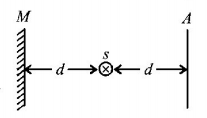
A.
$$\frac{{27{I_0}}}{9}$$
B.
$$\frac{{25{I_0}}}{9}$$
C.
$$\frac{{17{I_0}}}{9}$$
D.
$$\frac{{10{I_0}}}{9}$$
Answer :
$$\frac{{10{I_0}}}{9}$$
Solution :
$${E_1} = {I_0} = \frac{L}{{{d^2}}},{\text{without mirror}}$$
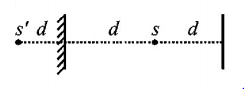
$${\text{and}}\,{E_2} = \frac{L}{{{d^2}}} + \frac{L}{{{{\left( {3d} \right)}^2}}} = \frac{L}{{{d^2}}}\left[ {1 + \frac{1}{9}} \right] = \frac{{10{I_0}}}{9}\,{\text{with}}\,{\text{mirror}}{\text{.}}$$
$${E_1} = {I_0} = \frac{L}{{{d^2}}},{\text{without mirror}}$$
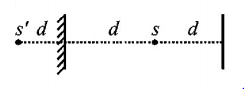
$${\text{and}}\,{E_2} = \frac{L}{{{d^2}}} + \frac{L}{{{{\left( {3d} \right)}^2}}} = \frac{L}{{{d^2}}}\left[ {1 + \frac{1}{9}} \right] = \frac{{10{I_0}}}{9}\,{\text{with}}\,{\text{mirror}}{\text{.}}$$