Question
The incentre of a triangle with vertices $$\left( {7,\,1} \right),\,\left( { - 1,\,5} \right)$$ and $$\left( {3 + 2\sqrt 3 ,\,3 + 4\sqrt 3 } \right)$$ is :
A.
$$\left( {3 + \frac{2}{{\sqrt 3 }},\,3 + \frac{4}{{\sqrt 3 }}} \right)$$
B.
$$\left( {1 + \frac{2}{{3\sqrt 3 }},\,1 + \frac{4}{{3\sqrt 3 }}} \right)$$
C.
$$\left( {7,\,1} \right)$$
D.
None of these
Answer :
$$\left( {3 + \frac{2}{{\sqrt 3 }},\,3 + \frac{4}{{\sqrt 3 }}} \right)$$
Solution :
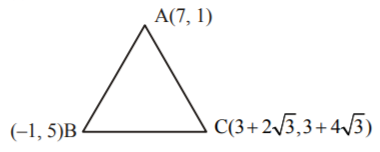
$$\because \,AB = BC = CA = 4\sqrt 5 ,$$
i.e., given triangle is equilateral.
(Incentre of a triangle are same as the centroid when triangle is equilateral)
Hence, incentre
$$\eqalign{ & = \left( {\frac{{7 - 1 + 3 + 2\sqrt 3 }}{3},\,\frac{{1 + 5 + 3 + 4\sqrt 3 }}{3}} \right) \cr & = \left( {3 + \frac{2}{{\sqrt 3 }},\,3 + \frac{4}{{\sqrt 3 }}} \right) \cr} $$
$$\because \,AB = BC = CA = 4\sqrt 5 ,$$
i.e., given triangle is equilateral.
(Incentre of a triangle are same as the centroid when triangle is equilateral)
Hence, incentre
$$\eqalign{ & = \left( {\frac{{7 - 1 + 3 + 2\sqrt 3 }}{3},\,\frac{{1 + 5 + 3 + 4\sqrt 3 }}{3}} \right) \cr & = \left( {3 + \frac{2}{{\sqrt 3 }},\,3 + \frac{4}{{\sqrt 3 }}} \right) \cr} $$