Question
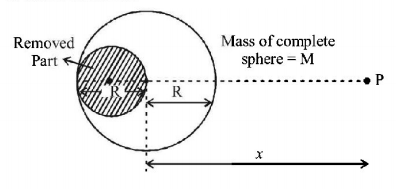
The gravitational field, due to the 'left over part’ of a uniform sphere (from which a part as shown, has been 'removed out’), at a very far off point, $$P,$$ located as shown, would be (nearly) :
The gravitational field, due to the 'left over part’ of a uniform sphere (from which a part as shown, has been 'removed out’), at a very far off point, $$P,$$ located as shown, would be (nearly) :
A.
$$\frac{5}{6}\frac{{GM}}{{{x^2}}}$$
B.
$$\frac{8}{9}\frac{{GM}}{{{x^2}}}$$
C.
$$\frac{7}{8}\frac{{GM}}{{{x^2}}}$$
D.
$$\frac{6}{7}\frac{{GM}}{{{x^2}}}$$
Answer :
$$\frac{7}{8}\frac{{GM}}{{{x^2}}}$$
Solution :
Let mass of smaller sphere (which has to be removed) is $$m$$
Radius $$ = \frac{R}{2}\,\left( {{\text{from figure}}} \right)$$
$$\frac{M}{{\frac{4}{3}\pi {R^3}}} = \frac{m}{{\frac{4}{3}\pi {{\left( {\frac{R}{2}} \right)}^3}}} \Rightarrow m = \frac{M}{8}$$
Mass of the left over part of the sphere
$$M' = M - \frac{M}{8} = \frac{7}{8}M$$
Therefore gravitational field due to the left over part of the sphere
$$ = \frac{{GM'}}{{{x^2}}} = \frac{7}{8}\frac{{GM}}{{{x^2}}}$$
Let mass of smaller sphere (which has to be removed) is $$m$$
Radius $$ = \frac{R}{2}\,\left( {{\text{from figure}}} \right)$$
$$\frac{M}{{\frac{4}{3}\pi {R^3}}} = \frac{m}{{\frac{4}{3}\pi {{\left( {\frac{R}{2}} \right)}^3}}} \Rightarrow m = \frac{M}{8}$$
Mass of the left over part of the sphere
$$M' = M - \frac{M}{8} = \frac{7}{8}M$$
Therefore gravitational field due to the left over part of the sphere
$$ = \frac{{GM'}}{{{x^2}}} = \frac{7}{8}\frac{{GM}}{{{x^2}}}$$