Question
The graph of the function $$y = f\left( x \right)$$ is symmetrical about the line $$x = 2,$$ then
A.
$$f\left( x \right) = - f\left( { - x} \right)$$
B.
$$f\left( {2 + x} \right) = f\left( {2 - x} \right)$$
C.
$$f\left( x \right) = f\left( { - x} \right)$$
D.
$$f\left( {x + 2} \right) = f\left( {x - 2} \right)$$
Answer :
$$f\left( {2 + x} \right) = f\left( {2 - x} \right)$$
Solution :
Let us consider a graph symm. with respect to line $$x = 2$$ as shown in the figure.
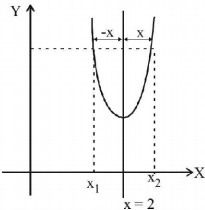
$$\eqalign{ & {\text{From the figure }}f\left( {{x_1}} \right) = f\left( {{x_2}} \right),\,{\text{where}}\,{x_1} = 2 - x\,{\text{and}}\,{x_2} = 2 + x \cr & \therefore f\left( {2 - x} \right) = f\left( {2 + x} \right) \cr} $$
Let us consider a graph symm. with respect to line $$x = 2$$ as shown in the figure.

$$\eqalign{ & {\text{From the figure }}f\left( {{x_1}} \right) = f\left( {{x_2}} \right),\,{\text{where}}\,{x_1} = 2 - x\,{\text{and}}\,{x_2} = 2 + x \cr & \therefore f\left( {2 - x} \right) = f\left( {2 + x} \right) \cr} $$