Question
The function $$f\left( x \right) = \frac{x}{{1 + x\tan \,x}}$$ has :
A.
one point of minimum in the interval $$\left( {0,\,\frac{\pi }{2}} \right)$$
B.
one point of maximum in the interval $$\left( {0,\,\frac{\pi }{2}} \right)$$
C.
no point of maximum, no point of minimum in the interval $$\left( {0,\,\frac{\pi }{2}} \right)$$
D.
two points of maxima in the interval $$\left( {0,\,\frac{\pi }{2}} \right)$$
Answer :
one point of maximum in the interval $$\left( {0,\,\frac{\pi }{2}} \right)$$
Solution :
$$\eqalign{ & f'\left( x \right) = \frac{{1 + x\tan \,x - x\left\{ {\tan \,x + x{{\sec }^2}x} \right\}}}{{{{\left( {1 + x\tan \,x} \right)}^2}}} = \frac{{1 - {x^2}{{\sec }^2}x}}{{{{\left( {1 + x\tan \,x} \right)}^2}}} \cr & f'\left( x \right) = 0\,\,\,\,\,\,\, \Rightarrow 1 - {x^2}{\sec ^2}x = 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \cos \,x = \pm x \cr} $$
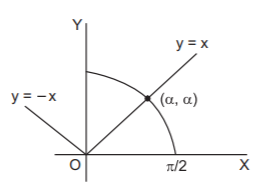
$$\therefore \,$$ in the interval $$\left( {0,\,\frac{\pi }{2}} \right),\,f'\left( x \right) = 0$$ can hold for only one value of $$x,$$ say $$\alpha, $$ where $$\cos \,\alpha = \alpha $$ (see the graph).
Verify $$f''\left( x \right) < 0{\text{ at }}x = \alpha $$
$$\eqalign{ & f'\left( x \right) = \frac{{1 + x\tan \,x - x\left\{ {\tan \,x + x{{\sec }^2}x} \right\}}}{{{{\left( {1 + x\tan \,x} \right)}^2}}} = \frac{{1 - {x^2}{{\sec }^2}x}}{{{{\left( {1 + x\tan \,x} \right)}^2}}} \cr & f'\left( x \right) = 0\,\,\,\,\,\,\, \Rightarrow 1 - {x^2}{\sec ^2}x = 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \cos \,x = \pm x \cr} $$
$$\therefore \,$$ in the interval $$\left( {0,\,\frac{\pi }{2}} \right),\,f'\left( x \right) = 0$$ can hold for only one value of $$x,$$ say $$\alpha, $$ where $$\cos \,\alpha = \alpha $$ (see the graph).

Verify $$f''\left( x \right) < 0{\text{ at }}x = \alpha $$