Question
The equation of the parabola whose focus is $$\left( {0,\,0} \right)$$ and the tangent at the vertex is $$x - y + 1 = 0$$ is :
A.
$${x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0$$
B.
$${x^2} - 4x + 4y - 4 = 0$$
C.
$${y^2} - 4x + 4y - 4 = 0$$
D.
$$2{x^2} + 2{y^2} - 4xy - x + y - 4 = 0$$
Answer :
$${x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0$$
Solution :
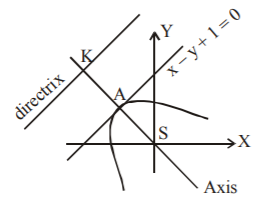
The length of the perpendicular drawn from the given focus upon the given line $$x - y + 1 = 0$$ is $$\frac{{0 - 0 + 1}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{{\sqrt 2 }}$$
The directrix is parallel to the tangent at the vertex.
So, the equation of the directrix is $$x - y + \lambda = 0,$$ where $$\lambda $$ is a constant to be determine.
But the distance between the focus and the directrix $$ = 2 \times $$ (the distance between the focus and the tangent at the vertex)
$$ = 2 \times \frac{1}{{\sqrt 2 }} = \sqrt 2 $$
Hence $$\frac{{0 - 0 + \lambda }}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 $$
$$\therefore \,\lambda = 2.$$ [$$\lambda $$ must be positive see figure]
$$\therefore $$ The directrix is the line $$x - y + 2 = 0.$$
Let $$\left( {x,\,y} \right)$$ be a moving point on the parabola. By the focus-directrix property of the parabola, its equation is
$$\eqalign{ & {\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {\left( { \pm \frac{{x - y + 2}}{{\sqrt 2 }}} \right)^2} \cr & {\text{or, }}\,{x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0 \cr} $$

The length of the perpendicular drawn from the given focus upon the given line $$x - y + 1 = 0$$ is $$\frac{{0 - 0 + 1}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{{\sqrt 2 }}$$
The directrix is parallel to the tangent at the vertex.
So, the equation of the directrix is $$x - y + \lambda = 0,$$ where $$\lambda $$ is a constant to be determine.
But the distance between the focus and the directrix $$ = 2 \times $$ (the distance between the focus and the tangent at the vertex)
$$ = 2 \times \frac{1}{{\sqrt 2 }} = \sqrt 2 $$
Hence $$\frac{{0 - 0 + \lambda }}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 $$
$$\therefore \,\lambda = 2.$$ [$$\lambda $$ must be positive see figure]
$$\therefore $$ The directrix is the line $$x - y + 2 = 0.$$
Let $$\left( {x,\,y} \right)$$ be a moving point on the parabola. By the focus-directrix property of the parabola, its equation is
$$\eqalign{ & {\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {\left( { \pm \frac{{x - y + 2}}{{\sqrt 2 }}} \right)^2} \cr & {\text{or, }}\,{x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0 \cr} $$