Question
The ellipse $${x^2} + 4{y^2} = 4$$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point $$\left( {4,\,0} \right).$$ Then the equation of the ellipse is :
A.
$${x^2} + 12{y^2} = 16$$
B.
$$4{x^2} + 48{y^2} = 48$$
C.
$$4{x^2} + 64{y^2} = 48$$
D.
$${x^2} + 16{y^2} = 16$$
Answer :
$${x^2} + 12{y^2} = 16$$
Solution :
The given ellipse is $$\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1$$
So $$A = \left( {2,\,0} \right)$$ and $$B = \left( {0,\,1} \right)$$
If $$PQRS$$ is the rectangle in which it is inscribed, then $$P = \left( {2,\,1} \right).$$
Let $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$
be the ellipse circumscribing the rectangle $$PQRS.$$
Then it passes through $$P\left( {2,\,1} \right)$$
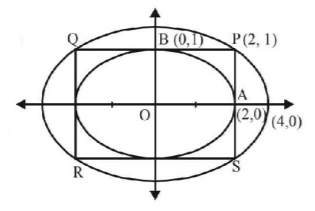
$$\therefore \frac{4}{{{a^2}}} + \frac{1}{{{b^2}}} = 1.....(a)$$
Also, given that, it passes through $$\left( {4,\,0} \right)$$
$$\eqalign{ & \therefore \frac{{16}}{{{a^2}}} + 0 = 1\,\,\,\, \Rightarrow {a^2} = 16 \cr & \Rightarrow {b^2} = \frac{4}{3}\left[ {{\text{substituting }}{a^2} = 16{\text{ in equation }}\left( a \right)} \right] \cr} $$
$$\therefore $$ The required ellipse is $$\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{{\frac{4}{3}}} = 1{\text{ or }}{x^2} + 12{y^2} = 16$$
The given ellipse is $$\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1$$
So $$A = \left( {2,\,0} \right)$$ and $$B = \left( {0,\,1} \right)$$
If $$PQRS$$ is the rectangle in which it is inscribed, then $$P = \left( {2,\,1} \right).$$
Let $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$
be the ellipse circumscribing the rectangle $$PQRS.$$
Then it passes through $$P\left( {2,\,1} \right)$$

$$\therefore \frac{4}{{{a^2}}} + \frac{1}{{{b^2}}} = 1.....(a)$$
Also, given that, it passes through $$\left( {4,\,0} \right)$$
$$\eqalign{ & \therefore \frac{{16}}{{{a^2}}} + 0 = 1\,\,\,\, \Rightarrow {a^2} = 16 \cr & \Rightarrow {b^2} = \frac{4}{3}\left[ {{\text{substituting }}{a^2} = 16{\text{ in equation }}\left( a \right)} \right] \cr} $$
$$\therefore $$ The required ellipse is $$\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{{\frac{4}{3}}} = 1{\text{ or }}{x^2} + 12{y^2} = 16$$