Question
The driver of a car travelling with speed $$30\,m{s^{ - 1}}$$ towards a hill sounds a horn of frequency $$600\,Hz.$$ If the velocity of sound in air is $$330\,m{s^{ - 1}},$$ the frequency of reflected sound as heard by driver is
A.
$$550\,Hz$$
B.
$$555.5\,Hz$$
C.
$$720\,Hz$$
D.
$$500\,Hz$$
Answer :
$$720\,Hz$$
Solution :
Use Doppler’s effect.
According to Doppler's effect, whenever there is a relative motion between a source of sound and the observer (listener), the frequency of sound heard by the observer is different from the actual frequency of sound emitted by source.
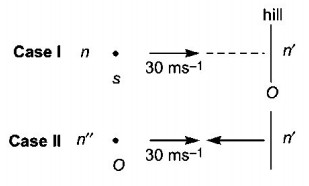
$$\eqalign{ & \left[ {{\text{for case }}1} \right] \cr & n' = \frac{v}{{v - 30}}n\,......\left( {\text{i}} \right) \cr} $$
\[\left[ {\begin{array}{*{20}{c}} {n = {\rm{frequency\,emitted\,by\,car}}}\\ {v = {\rm{velocity\,of\,sound}}} \end{array}} \right]\]
$$\eqalign{ & \left[ {{\text{for case }}2} \right] \cr & n'' = \frac{{v + 30}}{v}n'\,......\left( {{\text{ii}}} \right) \cr} $$
\[\left[ \begin{array}{l} n'' = {\rm{frequency\,heard\,by}}\\ {\rm{the\,driver\,after\,reflection}} \end{array} \right]\]
$$\eqalign{ & {\text{From Eqs}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right),{\text{ we get}} \cr & n'' = \frac{{v + 30}}{{v - 30}} = \frac{{360}}{{300}} \times 600 = 720\,Hz \cr} $$
Use Doppler’s effect.
According to Doppler's effect, whenever there is a relative motion between a source of sound and the observer (listener), the frequency of sound heard by the observer is different from the actual frequency of sound emitted by source.

$$\eqalign{ & \left[ {{\text{for case }}1} \right] \cr & n' = \frac{v}{{v - 30}}n\,......\left( {\text{i}} \right) \cr} $$
\[\left[ {\begin{array}{*{20}{c}} {n = {\rm{frequency\,emitted\,by\,car}}}\\ {v = {\rm{velocity\,of\,sound}}} \end{array}} \right]\]
$$\eqalign{ & \left[ {{\text{for case }}2} \right] \cr & n'' = \frac{{v + 30}}{v}n'\,......\left( {{\text{ii}}} \right) \cr} $$
\[\left[ \begin{array}{l} n'' = {\rm{frequency\,heard\,by}}\\ {\rm{the\,driver\,after\,reflection}} \end{array} \right]\]
$$\eqalign{ & {\text{From Eqs}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right),{\text{ we get}} \cr & n'' = \frac{{v + 30}}{{v - 30}} = \frac{{360}}{{300}} \times 600 = 720\,Hz \cr} $$