Question
The domain of definition of the function $$y = \frac{1}{{{{\log }_{10}}\left( {1 - x} \right)}} + \sqrt {x + 2} $$ is
A.
$$\left( { - 3,\, - 2} \right)$$ excluding $$-2.5$$
B.
$$\left[ {0,1} \right]$$ excluding 0.5
C.
$$\left[ { - 2,1} \right)$$ excluding 0
D.
none of these
Answer :
$$\left[ { - 2,1} \right)$$ excluding 0
Solution :
$$\eqalign{ & y = \frac{1}{{{{\log }_{10}}\left( {1 - x} \right)}} + \sqrt {x + 2} \cr & y = f\left( x \right) + g\left( x \right) \cr} $$
NOTE THIS STEP: Then domain of given function is $${D_f} \cap {D_g}$$
Now, for domain of $$f\left( x \right) = \frac{1}{{{{\log }_{10}}\left( {1 - x} \right)}}$$
We know it is defined only when $$1 - x > 0$$ and $$1 - x \ne 1 \Rightarrow x < 1\,{\text{and}}\,x \ne 0$$
$$\eqalign{ & \therefore {D_f} = \left( { - \infty ,1} \right) - \left\{ 0 \right\} \cr & {\text{For}}\,{\text{domain}}\,{\text{of}}\,g\left( x \right) = \sqrt {x + 2} \cr & x + 2 \geqslant 0 \cr & \Rightarrow x \geqslant - 2 \cr & \therefore {D_g} = \left[ { - 2,\infty } \right) \cr} $$
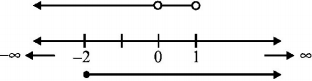
$$\therefore $$ Common domain is $$\left[ { - 2,1} \right) - \left\{ 0 \right\}$$
$$\eqalign{ & y = \frac{1}{{{{\log }_{10}}\left( {1 - x} \right)}} + \sqrt {x + 2} \cr & y = f\left( x \right) + g\left( x \right) \cr} $$
NOTE THIS STEP: Then domain of given function is $${D_f} \cap {D_g}$$
Now, for domain of $$f\left( x \right) = \frac{1}{{{{\log }_{10}}\left( {1 - x} \right)}}$$
We know it is defined only when $$1 - x > 0$$ and $$1 - x \ne 1 \Rightarrow x < 1\,{\text{and}}\,x \ne 0$$
$$\eqalign{ & \therefore {D_f} = \left( { - \infty ,1} \right) - \left\{ 0 \right\} \cr & {\text{For}}\,{\text{domain}}\,{\text{of}}\,g\left( x \right) = \sqrt {x + 2} \cr & x + 2 \geqslant 0 \cr & \Rightarrow x \geqslant - 2 \cr & \therefore {D_g} = \left[ { - 2,\infty } \right) \cr} $$

$$\therefore $$ Common domain is $$\left[ { - 2,1} \right) - \left\{ 0 \right\}$$