Question
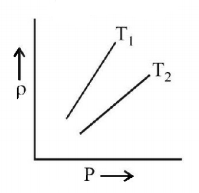
The density $$\left( \rho \right)$$ versus pressure $$\left( P \right)$$ of a given mass of an ideal gas is shown at two temperatures $${T_1}$$ and $${T_2}$$ Then relation between $${T_1}$$ and $${T_2}$$ may be
The density $$\left( \rho \right)$$ versus pressure $$\left( P \right)$$ of a given mass of an ideal gas is shown at two temperatures $${T_1}$$ and $${T_2}$$ Then relation between $${T_1}$$ and $${T_2}$$ may be
A.
$${T_1} > {T_2}$$
B.
$${T_2} > {T_1}$$
C.
$${T_1} = {T_2}$$
D.
All the three are possible
Answer :
$${T_2} > {T_1}$$
Solution :
According to ideal gas equation
$$\eqalign{ & PV = nRT \cr & PV = \frac{m}{M}RT,P = \frac{\rho }{M}RT\,\,{\text{or}}\,\,\frac{\rho }{P} = \frac{M}{{RT}} \cr & {\text{or}}\,\,\frac{\rho }{P} \propto \frac{1}{T} \cr} $$
Here, $$\frac{\rho }{P}$$ represent the slope of graph
Hence $${T_2} > {T_1}$$
According to ideal gas equation
$$\eqalign{ & PV = nRT \cr & PV = \frac{m}{M}RT,P = \frac{\rho }{M}RT\,\,{\text{or}}\,\,\frac{\rho }{P} = \frac{M}{{RT}} \cr & {\text{or}}\,\,\frac{\rho }{P} \propto \frac{1}{T} \cr} $$
Here, $$\frac{\rho }{P}$$ represent the slope of graph
Hence $${T_2} > {T_1}$$