Question
The centre of the circle passing through the point (0, 1) and touching the curve $$y = {x^2}$$ at $$\left( {2,\,4} \right)$$ is-
A.
$$\left( {\frac{{ - 16}}{5},\,\frac{{27}}{{10}}} \right)$$
B.
$$\left( {\frac{{ - 16}}{7},\,\frac{{53}}{{10}}} \right)$$
C.
$$\left( {\frac{{ - 16}}{5},\,\frac{{53}}{{10}}} \right)$$
D.
none of these
Answer :
$$\left( {\frac{{ - 16}}{5},\,\frac{{53}}{{10}}} \right)$$
Solution :
Let $$C\left( {h,\,k} \right)$$ be the centre of circle touching $${x^2} = y$$ at $$B\left( {2,\,4} \right).$$ Then equation of common tangent at $$B$$ is
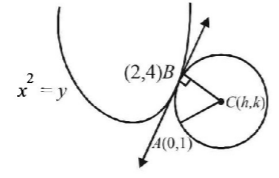
$$2.x = \frac{1}{2}\left( {y + 4} \right)\,\,i.e.,\,\,\,4x - y = 4$$
Radius is perpendicular to this tangent
$$\eqalign{ & \therefore 4\left( {\frac{{k - 4}}{{h - 2}}} \right) = - 1\,\, \Rightarrow 4k = 18.....(1) \cr & {\text{Also }}\,AC = BC \cr & \Rightarrow {h^2} + {\left( {k - 1} \right)^2} = {\left( {h - 2} \right)^2} + {\left( {k - 4} \right)^2} \cr & \Rightarrow 4h + 6k = 19.....(2) \cr} $$
Solving (1) and (2) we get the centre as $$\left( {\frac{{ - 16}}{5},\,\frac{{53}}{{10}}} \right)$$
Let $$C\left( {h,\,k} \right)$$ be the centre of circle touching $${x^2} = y$$ at $$B\left( {2,\,4} \right).$$ Then equation of common tangent at $$B$$ is

$$2.x = \frac{1}{2}\left( {y + 4} \right)\,\,i.e.,\,\,\,4x - y = 4$$
Radius is perpendicular to this tangent
$$\eqalign{ & \therefore 4\left( {\frac{{k - 4}}{{h - 2}}} \right) = - 1\,\, \Rightarrow 4k = 18.....(1) \cr & {\text{Also }}\,AC = BC \cr & \Rightarrow {h^2} + {\left( {k - 1} \right)^2} = {\left( {h - 2} \right)^2} + {\left( {k - 4} \right)^2} \cr & \Rightarrow 4h + 6k = 19.....(2) \cr} $$
Solving (1) and (2) we get the centre as $$\left( {\frac{{ - 16}}{5},\,\frac{{53}}{{10}}} \right)$$