Question
The area of the smaller segment cut off from the circle $${x^2} + {y^2} = 9$$ by $$x = 1$$ is :
A.
$$\frac{1}{2}\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
B.
$$\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
C.
$$\left( {\sqrt 8 - 9\,{{\sec }^{ - 1}}3} \right){\text{sq}}{\text{.unit}}$$
D.
None of the above
Answer :
$$\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
Solution :
Given, equation of the circle is $${x^2} + {y^2} = 9$$
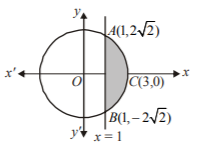
$$\therefore $$ Area of the smaller segment cut off from the circle $${x^2} + {y^2} = 9$$ by $$x = 1,$$ is given by
$$\eqalign{ & A = 2\int_1^3 {\sqrt {9 - {x^2}} } dx \cr & \,\,\,\,\, = 2.\frac{1}{2}\left[ {x\sqrt {9 - {x^2}} + 9\,{{\sin }^{ - 1}}\frac{x}{3}} \right]_1^3 \cr & \,\,\,\,\, = \left[ {3.\sqrt {9 - 9} + 9\,{{\sin }^{ - 1}}\left( {\frac{3}{3}} \right) - 1.\sqrt {9 - 1} - 9\,{{\sin }^{ - 1}}\left( {\frac{1}{3}} \right)} \right] \cr & \,\,\,\,\, = \left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}} \cr} $$
Given, equation of the circle is $${x^2} + {y^2} = 9$$
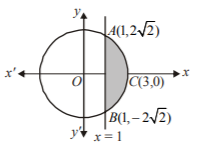
$$\therefore $$ Area of the smaller segment cut off from the circle $${x^2} + {y^2} = 9$$ by $$x = 1,$$ is given by
$$\eqalign{ & A = 2\int_1^3 {\sqrt {9 - {x^2}} } dx \cr & \,\,\,\,\, = 2.\frac{1}{2}\left[ {x\sqrt {9 - {x^2}} + 9\,{{\sin }^{ - 1}}\frac{x}{3}} \right]_1^3 \cr & \,\,\,\,\, = \left[ {3.\sqrt {9 - 9} + 9\,{{\sin }^{ - 1}}\left( {\frac{3}{3}} \right) - 1.\sqrt {9 - 1} - 9\,{{\sin }^{ - 1}}\left( {\frac{1}{3}} \right)} \right] \cr & \,\,\,\,\, = \left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}} \cr} $$